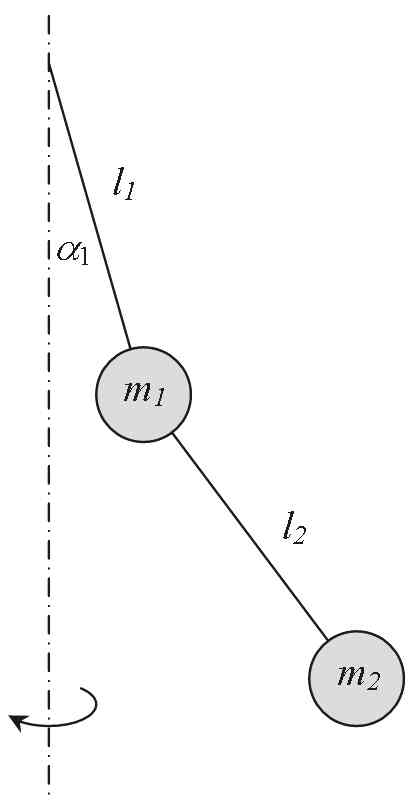
Deel I KINEMATICA

I.1 Inleidende begrippen

1. Bepaal de afgelegde weg en de verplaatsing als je van school naar huis gaat. Gebruik een landkaartje voor deze oefening.

2. Bepaal de gemiddelde snelheid als je naar huis gaat.

3. Zet onderstaande grootheden in de gevraagde eenheid.
   

   800 mm	= ............... m
   5 km	= ............... m
   200 hm	= ............... m
   35000 mm	= ............... km
   0,2 km/min	= ............... m/s
   10 m/min	= ............... m/s
   25 m/s	= ............... km/h
   80 km/h	= ............... m/s
   65 kg	= ............... g
   500 g	= ............... kg
   125 s	= ............... min
   2 h 35 min 10 s	= ............... s
   12568 s	= ......h ..... min .....s
   35 km/min²	= ............... m/s²

I.2 De eenparige rechtlijnige beweging

1. Een wandelaar en een jogger bevinden zich op 1 km van elkaar en lopen naar elkaar toe. De jogger vertrekt 100 seconden na de wandelaar en zijn snelheid is dubbel zo groot. Ze ontmoeten elkaar op 400 meter van het vertrekpunt van de wandelaar. Bereken nu de snelheid van wandelaar en de jogger.

2. Op een werkstuk wordt schroefdraad gesneden over een afstand van 250 mm. De snelheid van de sledecombinatie bedraagt 5 mm/s. Hoeveel tijd heb je nodig om óón pas te draaien.

I.3 De eenparige cirkelvormige beweging

1. Je draait een werkstuk, diameter 120 mm, met een hardmetalen beitel. De rotatiefrequentie van de draaibank heb je ingesteld op 300 /min. Bepaal de snijsnelheid in m/min.

I.4 Samenstellen en ontbinden van bewegingen

1. Je wil een rivier met een breedte van 100 m overzwemmen. Omdat je loodrecht wil oversteken zwem je onder een hoek van 75° stroomopwaarts. De relatieve zwemsnelheid is 1,5 m/s en de stroomsnelheid is 0,5 m/s. Bij aankomst merk je dat de overtocht niet loodrecht is gebeurd. Hoeveel meter van je doel kom je aan? Hoelang heb je nodig gehad om de rivier over te zwemmen?

   

2. Bij de opslag van Kim Clijsters vertrekt de tennisbal op een hoogte van 2,5 m met een snelheid van 180 km/h onder een hoek van 5° naar beneden. Gaat de bal over het net en waar zal de tennisbal de grond raken? De opslag gebeurt 12 meter voor het net en het net is 0,914 meter hoog.

3. Een tennisbal werp je weg onder een hoek van 30°. Na een bepaalde tijd, t, raakt de bal de grond. Onder welke hoek moet je deze tennisbal met dezelfde snelheid gooien zodat hij na een tijd 2.t de grond raakt. Er is geen luchtweerstand.

4. Je gooit een steen weg onder een hoek van 45°. De steen komt neer op een afstand s_max. Onder welke hoek moet je de steen weggooien, met dezelfde beginsnelheid, zodat de worpafstand gelijk is aan s_max/2.

I.5 De eenparig veranderlijke rechtlijnige beweging

1. Een straaljager die vertrekt heeft een snelheid nodig van 216 km/h om op te stijgen. Je veronderstelt voor de beweging van de straaljager een constante versnelling. De startbaan is 300 m lang. Bepaal de versnelling van de straaljager en de tijd die nodig is om op te stijgen.

2. Een kusttram met een massa van 40 ton rijdt met een snelheid van 50 km/h langs de zee. De kusttram moet plots stoppen en staat 96 m verder volledig stil. Bepaal de vertraging en de remtijd van de kusttram. Hoe groot is de snelheid van de kusttram na 60 m.

3. Je werpt verticaal een steen omhoog. De steen valt 5 s later op de grond. Bereken de verticale beginsnelheid van de steen.

I.6 Beweging van lichamen

1. Kruk OA van een drijfstangmechanisme is 30 mm lang. De kruk draait eenparig rond met een rotatiefrequentie van 20 /min. Bepaal de snelheid van zuiger B op het ogenblik dat de kruk een hoek maakt van 30° met de horizontale as. De lengte van drijfstang AB is 75 mm. De zuiger staat onder een hoek van 15° met de horizontale as. Los dit grafisch en analytisch op.

   

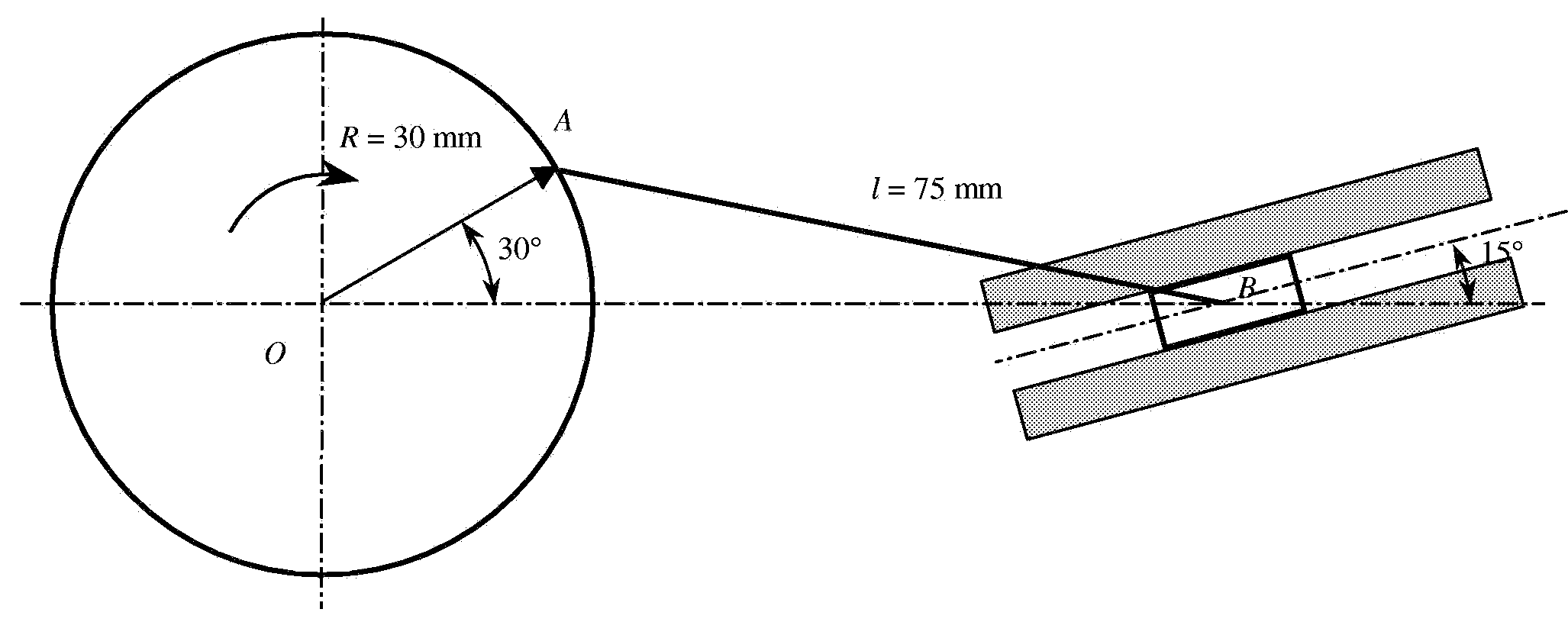
Deel II STATICA

II.1 De wetten van Newton

1. Een lichaam met een massa van 50 kg bevindt zich op verschillende planeten. Bepaal de zwaartekracht van dit lichaam op: de aarde, de maan, mars, venus? Zoek de waarde van g op in een naslagwerk of op internet.

2. Teken op schaal een kracht van 8000 N. De werklijn maakt een hoek van 25° met de x-as. Hoe schrijf je deze kracht vectorieel?

II.2 Samenstellen van samenlopende krachten

1. Bereken de resulterende kracht van vier samenlopende coplanaire krachten die aangrijpen in óón punt, F₁ = 2 kN, F₂ = 4 kN, F₃ = 3 kN en F₄ = 5 kN.
   F₁ werkt horizontaal naar rechts,
   F₂ maakt een hoek van 30° met F₁ (tegenwijzerzin),
   F₃ maakt een hoek van 80° met F₂ (tegenwijzerzin),
   F₄ werkt verticaal naar beneden.

2. Bepaal de krachten die optreden in kabel AB en staaf BC als in punt B een last hangt van 10 kN.

   

3. Bepaal de krachten die optreden in ketting AB en staaf BC als in punt B een last hangt met een massa van 5 000 kg.

   

4. Aan een takel hangt een vat van 1000 kg. Bij de takel zijn AC en BC stangen en is DC een stalen kabel. Bepaal de krachten in de stangen en de kabel. De coördinaten, in meter, zijn: A(0; 0; 2), B(0; 0; -2), C(2; 1,5; 0) en D(-2; 0; 0).

   

II.3 Moment van een kracht

1. Bereken het resulterende moment van onderstaande drie krachten. Teken dit moment als vector op onderstaande figuur. F₁ = 300 N grijpt aan in punt A(3; 2), F₂ = 220 N grijpt aan in punt B(0; 4) en F₃ (F_3x = -200 N en F_3y = 100 N) grijpt aan in punt C(-2; -3)

   

II.4 De momentenstelling en haar toepassingen

1. Bepaal het zwaartepunt van onderstaande figuur. Teken het zwaartepunt op de figuur.
   

II.5 Kopppel van krachten

1. Een kracht van 1000 N werkt op een steunblok van een pneumatische cilinder. Wat zijn de krachten op de bouten in A en B? Bout B zit in een gleuf.

   

II.6 Evenwicht van lichamen

1. Op een wig liggen 2 massa's die verbonden zijn met een koord. Bepaal de massa van lichaam 2 zodat dit lichaam naar beneden schuift. De wrijvingfactor tussen lichaam 1 en de wig is 0,4 en tussen lichaam 2 en de wig 0,25. m₁ = 200 kg

   

2. Een valluik heeft een massa van 20 kg. Via een katrolsysteem is het luik verbonden met een massa van 8 kg. Hoe groot is de openingshoek?
   

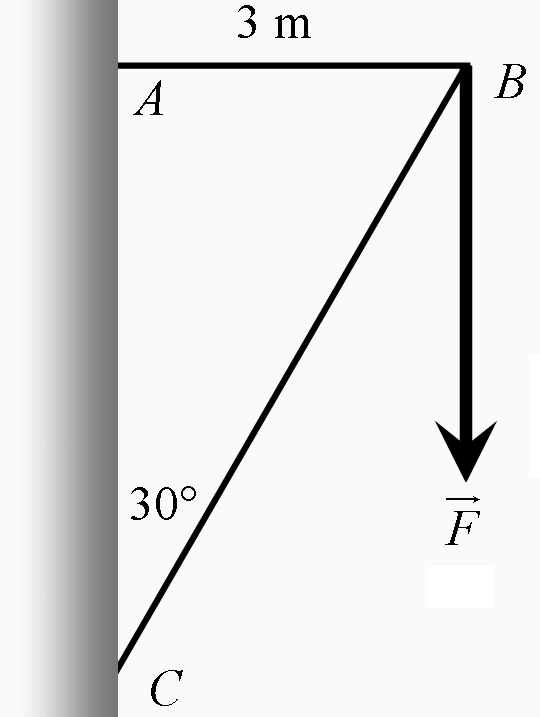
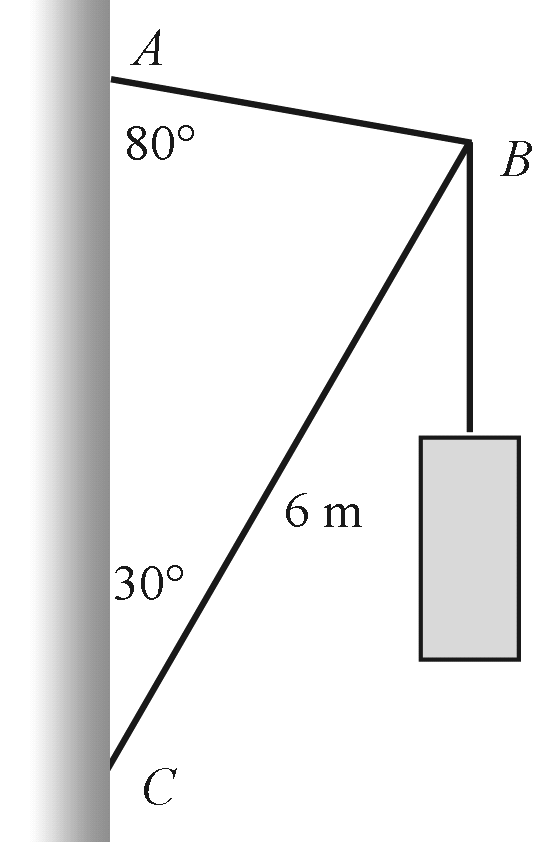
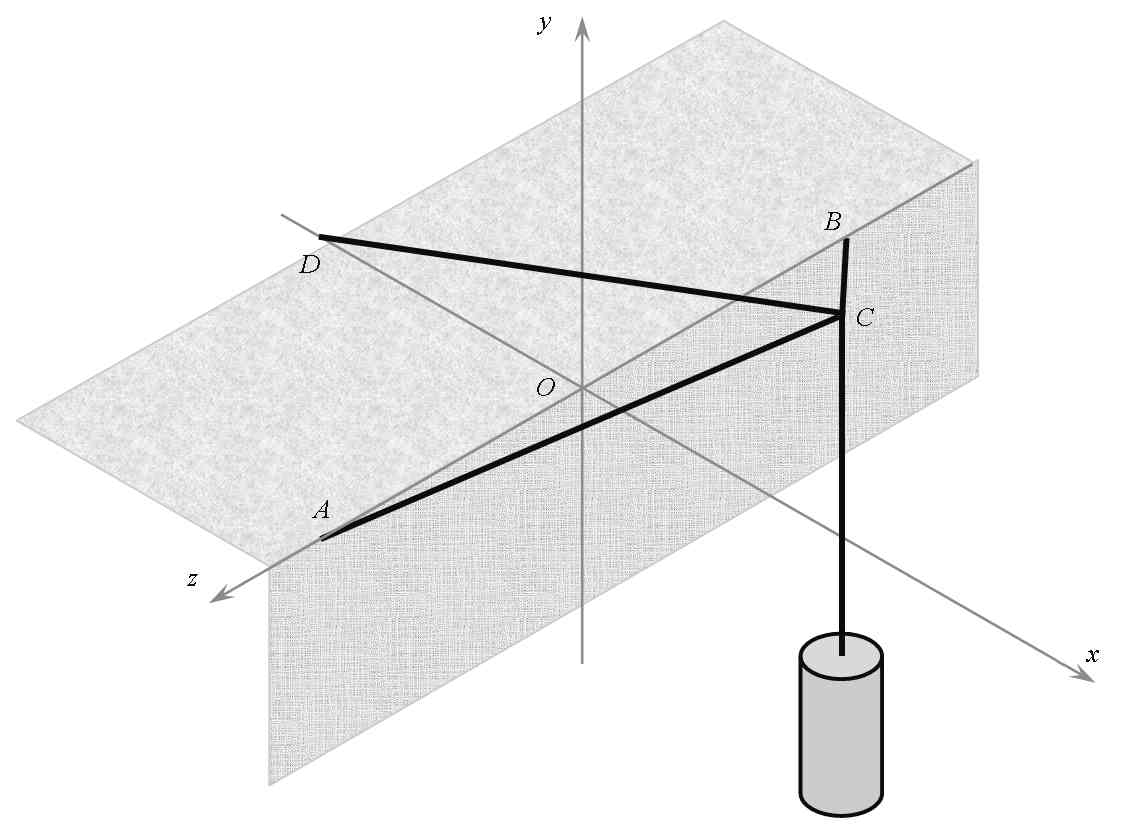
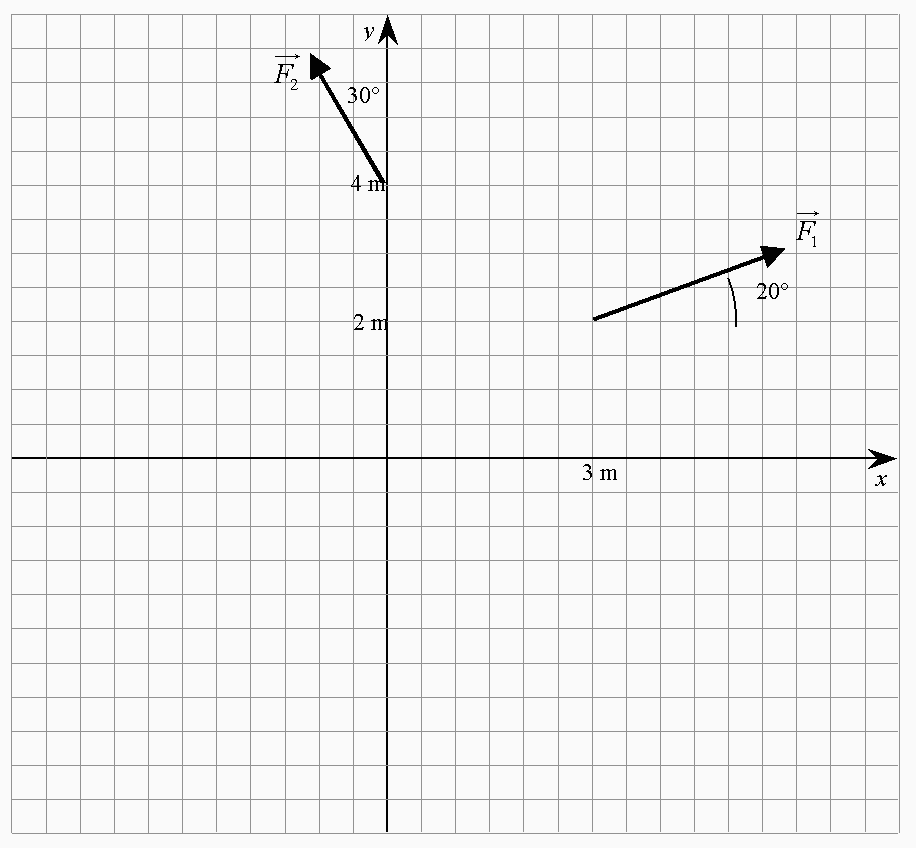
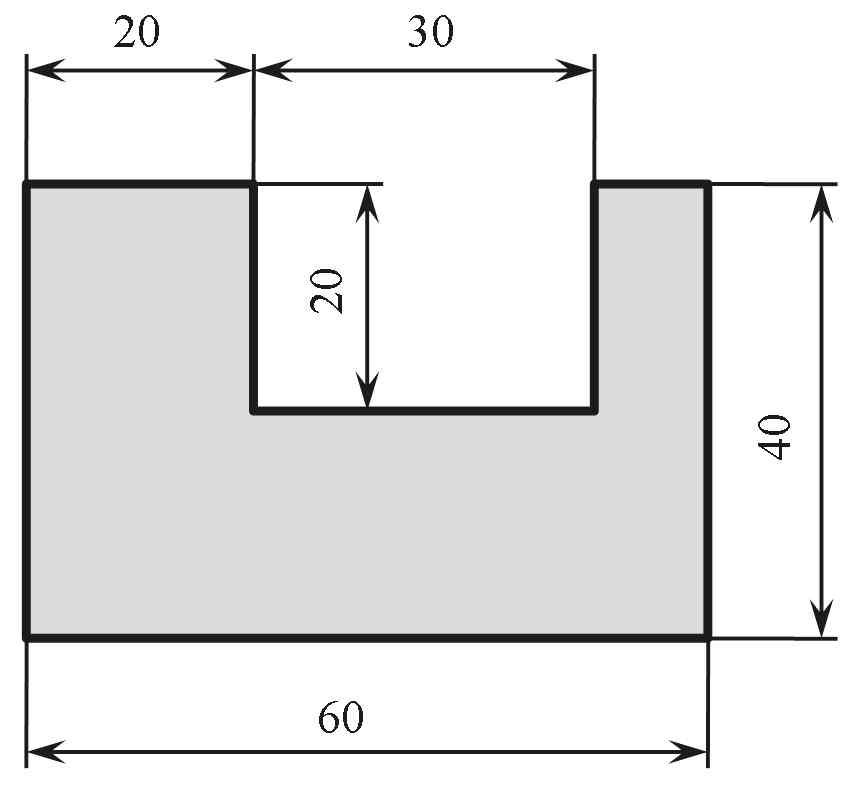
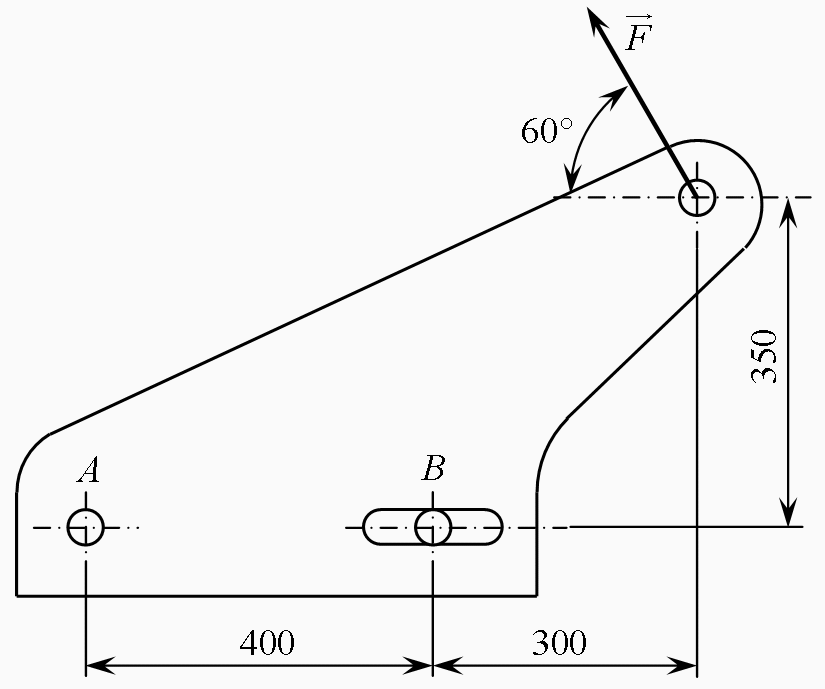
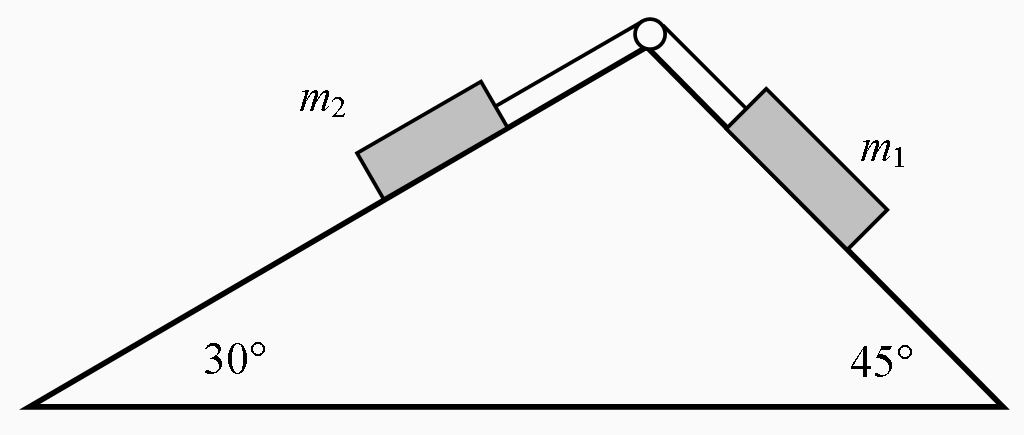
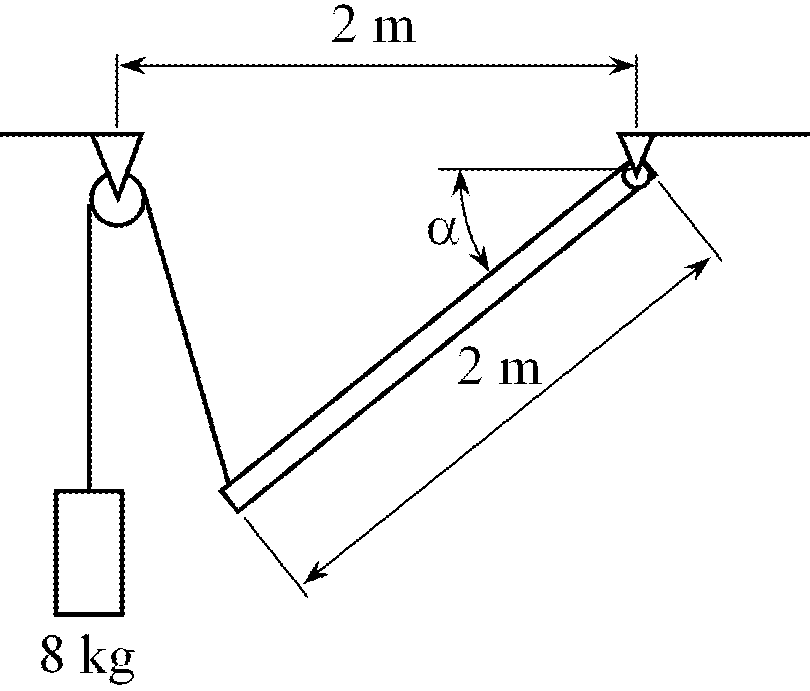
DEEL III DYNAMICA

III.1 Dynamica van een lichaam

1. Je zit in en luchtballon die stilhangt en een dynamometer bepaalt je gewicht, 600 N. Op een bepaald moment geeft de dynamometer een kracht aan van 550 N. Wat weet je over de beweging van de luchtballon op dat moment?

2. Een jongen met een gewicht van 800 N staat in een lift op een weegschaal. Als de lift begint te bewegen leest de jongen 850 N af op de weegschaal. Bepaal de versnelling van de lift.

III.2 Centripetale kracht

1. Aan het uiteinde van een touw wordt een bol met een massa van 3 kg bevestigd en in een horizontaal vlak rondgeslingerd met een straal van 1 m. Het touw breekt bij een trekkracht van 80 N. Bereken de maximale rotatiefrequentie waarmee de bol rondgeslingerd kan worden.

2. Een steen met een massa van 2 kg is vastgemaakt aan een koord van 80 cm. De steen draait rond met een eenparige cirkelvormige beweging in een horizontaal vlak. De tijd die nodig is om óón cirkelbeweging te maken bedraagt 0,3 s. Bereken de spankracht in de koord.

3. Een voorwerp ligt op een horizontale draaitafel op 0,60 m van het middelpunt. De wrijvingsfactor tussen het voorwerp en de draaitafel is 0,30. Wat is de maximale snelheid van het voorwerp zodat het niet van de draaitafel afschuift?

4. Twee massa's zijn met elkaar verbonden zoals op onderstaande figuur. Door een ronddraaiende beweging maakt l₁ met de rotatieas een hoek van 20°. Bepaal de rotatiefrequentie van het geheel. m₁ = 2 kg, m₂ = 2 kg, l₁ = 1 m en l₂ = 1 m.
   _{Tip: los moeilijke vergelijking numerisch of m.b.v. een grafisch rekentoestel op.}

   

III.3 Energie

1. Aan veer A, veerconstante k_A, hangt een bol met massa m. De veer rekt uit over een afstand l. Aan veer B wordt dezelfde bol gehangen, de veerconstante is tweemaal kleiner dan k_A. Bereken de verhouding van potentiële energie bij evenwicht.

2. Een elastiek wordt met óón uiteinde aan het plafond bevestigd. Aan het andere uiteinde is een steen vastgemaakt die 60 N weegt. De lengte van het onbelaste elastiek is 1,00 m, zijn veerconstante bedraagt 160 N/m. Het elastiek wordt verticaal naar beneden uitgerekt tot het 1,50 m lang is. Vanuit die stand wordt het geheel zonder beginsnelheid losgelaten. Het elastiek wordt massaloos verondersteld. Bereken de hoogte dat de steen maximaal zal opstijgen.

3. Een veer wordt uitgerekt door een kracht. Bereken de verhouding van de arbeid geleverd door deze kracht bij een uitrekking van 10 mm tot 20 mm tot de arbeid bij een uitrekking van 0 mm tot 10 mm.

III.4 Impuls, krachtstoot

1. Een auto met een massa van 1000 kg rijdt met een snelheid van 70 km/h tegen een muur en komt na 0,25 s tot stilstand. Bepaal de gemiddelde kracht gedurende de botsing. Bereken de botsingsenergie.

Top