3.

Getallenleer/-theorie

3.1.

Het getal

In het dagelijkse leven heeft iedereen wel iets te maken met getallen. Of het nu de hoeveelheid boterhammen is, die men ’s morgens eet of men berekent de doorhanging van een brug.
Overal worden getallen gebruikt. Maar wat is een getal en welke soorten getallen bestaan er?

Een getal is een abstracte, symbolische, weergave van een aantal of een hoeveelheid, bijvoorbeeld:

• 3 boterhammen bij het ontbijt.
• 4,5 centimeter doorhanging van de brug.
• 240 liter water in een regenton.

Een getal is niet hetzelfde als een cijfer. Cijfers zijn symbolen waarmee getallen voorgesteld worden.
De cijfers die wij kennen zijn 0, 1, 2 , 3, 4, 5, 6, 7, 8 en 9.
Een getal bestaat uit 1 één of meerdere cijfers, zoals: 4, 12, 543.

3.2.

Getalverzamelingen

In de wiskunde bestaan verschillende verzamelingen van getallen.

3.2.1

Natuurlijke getallen

De eenvoudigste getallen zijn natuurlijke getallen. Natuurlijke getallen zijn de getallen waarmee we tellen: 1, 2, 3, 4, 5, …. Dus positieve hele getallen.
De verzameling van alle natuurlijke getallen wordt N genoemd en als volgt weergegeven

Het getal nul behoort niet tot de verzameling van natuurlijke getallen. Dit in tegenstelling van wat vaak wel wordt aangenomen.
Wil je wel het getal nul in de verzameling betrekken, dan dient dit als volgt weergegeven te worden:

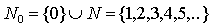
Verzameling No bevat het element nul én de verzameling van positieve gehele getallen. Het symbool È betekent: het verenigen van 2 verzamelingen. De bovenstaande weergave wil dus zeggen: de vereniging van de verzameling No met verzameling N geeft de totale verzameling: 0, 1, 2, 3, 4, 5,...

3.2.2

Gehele getallen

De natuurlijke getallen voldoen uitstekend voor het optellen van b.v. schapen of muntstukken.
De hindoes hadden opgemerkt dat 8 minus 3 duidelijk 5 was, maar 3 minus 8 was niet zo simpel. Het antwoord is een negatief getal, n.l. -5. Dit is geen element van N.
Een negatief getal is wat moeilijker te begrijpen, want een gewicht van -5 kilo kan niet.
Er ontstond een nieuwe verzameling Z.
De negatieve getallen tesamen met de natuurlijke getallen is de verzameling van de gehele getallen.

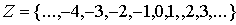
Let op: het betreft alleen gehele getallen, dus zonder decimalen, breuken, e.d.

3.2.3

Rationale getallen

Bij deling van gehele getallen ontdekte men dat niet alle delingen uitkwamen op een geheel getal. 8 gedeeld door 4 is gelijk aan 2, maar vier gedeeld door 8 geeft als antwoord 1/2.
Dit is geen geheel getal, maar een breuk. Een breuk is een geheel getal gedeeld door een geheel getal, b.v.3/8, 6/13, etc. Breuken zijn niet als gehele getallen te schrijven.
Alle breuken samen noemt men: de rationale getallen.

Zet je de breuken om naar decimalen, dan zijn er twee mogelijkheden:

1. Het aantal decimalen is eindig, b.v.: 0,25, 0,125,...
2. In de decimalen zit een herhaling, b.v.: 11,21818181818... (617/55)

De verzameling van rationale getallen wordt als volgt omschreven:

a en b zijn elementen van N
b is ongelijk aan 0.

Let op: een getal is alleen rationaal als deze geschreven kan worden als een breuk!

3.2.4

Irrationale getallen

Een irrationaal getal is een getal die niet rationaal is. Dat wil dus zeggen: een getal die niet als een breuk geschreven kan worden.
Een voorbeeld van een irrationale getal is de wortel uit 2.

3.2.5

Reeële getallen

 De rationale en irrationale getallen samen vormen de verzameling van reële getallen.
Bijna alle getallen, o.a. gebruikt op school, zijn reële getallen. Ze kunnen geschreven worden als decimalen.

3.2.6

Transcedente getallen

Een reëel getal dat niet algebraïsch is, noemt men transcedent.
Een transcedent getal dus niet te schrijven is als decimalen.

Er zijn veel transcedente getallen. Enkele voorbeelden zijn:

1. pi = 3,14159....
2. e = 2,71828....

3.2.7

Imaginaire getallen

3.2.8

Complexe getallen

3.3.

Getallenstelsels

3.4.

Bijzondere getallen

3.4.1

Het getal nul

Het getal nul neemt een bijzondere plaats in. De nul vervult, in de wiskunde, twee functies:

1. De nul stelt ons in staat onderscheid te maken tussen getallen als 51 en 501
2. De nul staat voor: niets

In de vroegere, toegepast in de westerse wereld, bestond het getal nul niet. Het getal nul werd door de griekse filosofen genegeerd en hadden zelfs gepleit om nul buiten de wet te stellen, omdat de samenhang van de andere getallen doorbrak. Het delen van een gewoon getal door nul gaf een onbegrijpelijke uitkomst.

Het huidige tientallige getallenstelsel, wat we hanteren, is een positiestelsel. De positie van het cijfer bepaalt de waarde van deze cijfer. B.v een honderdtal of een tiental. Een voorbeeld:
501 = 5 x 100 + 0 x 10 + 1
De Egyptische of het romeinse getallenstelsel is geen getallenstelsel. D.m.v. symbolen wordt het aantal gegeven.
Voorbeeld:

I= 1 V = 5 X = 10 C = 100 L = 500 M = 1000

MCCCXVI

= 1xM + 3xC + 1xX + 1xV + 1xI = 1000 + 3x100 + 10 + 5 + 1 = 1316

Hier is te zien dat waarde L niet is toegepast.
In deze stelsels is geen nul nodig. Omdat in de westerse lange tijd de romeinse getallenstelsel gehanteerd werd, is het getal nul nooit gebruikt.
Mede door de franse geleerde Gerbert de Aurillac, in de tiende eeuw, zijn we het, indo-arabische, tientallige getallenstelsel gaan gebruiken. De nul werd nog steeds niet gebruikt. Op de positie waar de nul zou moeten komen staan werd een ledige plaats gebruikt.
In de loop der tijd zal ik dit verhaal afmaken, want er rest nog een vraag: waarom is men de nul gaan gebruiken?

3.4.1

Volmaakte getallen

De 'Pythagorische broederschap', opgericht door Pythagoras, zocht onder de oneindig hoeveelheid getallen, naar getallen die een speciale betekenis hadden. Sommige van de meest bijzondere waren de zogenaamde 'volmaakte getallen'.
Numeriek volmaaktheid is afhankelijk van de delers van het getal. Delers zijn getallen die, zonder rest, deelbaar zijn op het originele getal.
Bijvoorbeeld: de delers van 12 zijn 1, 2, 3, 4 en 6. Is de som van de delers groter dan het getal zelf, dan wordt het getal een 'excessief getal' genoemd. 12 is een excessief getal, want de som van zijn delers is 1+2+3+4+6 = 16.

Is de som van de delers kleiner dan het getal zelf, dan noemt men dit een deficiënt getal.
Bijvoorbeeld het getal 10. De delers zijn 1,2 en 5. Bij elkaar opgeteld is dit 8.

De meest bijzondere en zeldzaamste getallen, zijn die getallen waarbij de som van de delers gelijk is aan het getal zelf.
Deze getallen noemt men volmaakte getallen. Het getal 6 is zo'n getal. Het getal 6 heeft als delers: 1, 2 en 3. Tellen we deze getallen opdan krijg je weer het getal 6.
Het eerst volgend getal is 28, want de delers opgeteld is: 1+2+4+7+14 = 28

Naarmate de natuurlijke getallen groter worden, wordt het vinden van volmaakte getallen moeilijker. Het derde volmaakt getal is 496, het vierde is 8128, vijfde is 33.550.336 en het zesde getal is 8.589.869.056.

Behalve dat ze de som van hun delers zijn, vertonen de volmaakte getallen ook andere eigenschappen.
B.v.: volmaakte getallen zijn altijd de som van een reeks opeenvolgende natuurlijke getallen:

3.4.1

Bevriende getallen

3.x.