The Generation Format

Chunks of Won and Lost Info

The tablebase is stored in two sections: the won info for wtm positions, and the lost(N) info for btm. We use different formats for both, as the won info is difficult to compress (during most of the generation around 50% of the positions is won), and we don't want to specify it by winning distance. So we store the plain bitmaps for this info, 1 bit per position, which is overwritten by the updated bitmap after every cycle. The lost(N) data will be differentiated by the winning distance N, which can be measured by any metric one desires. For most N it is sparse to extremely sparse, as even in generally-won endgames where black has 2 or 3 men, the lost btm poitions hardly ever total more than 40%, and are distibuted over many N. At its peak it will be ~5%, and in lengthy end-games there are many generations where it is 0.1-0.01%. So this data is highly compressible, and will be stored as Run-Length coded data, where the run length itself is compressed at one or two per byte, or (for large empty areas) as a series of spacer codes.

Both the won and the lost data is subdivided into 'chunks'. A chunk represents the smallest unit that is read or written, and is a 4-men slice of the entire TB. Each chunk is stored contiguousy on the hard disk. This means that the 7-men TB can be considered a 3-dimensional array of chunks, indexed by the square numbers of the first 3 pieces (which must be all white). A cycle will consist of gathering successive slices of the TB in memory by reading all chunks belonging to the slice, processing moves that stay within the loaded slice, and writing the updated info back to the TB. Typically one of the white pieces will be kept fixed (static) to define a slice; to process the moves of that piece, the TB will have to be traversed again, this time gathering different slices, which keep another piece fixed, so that the piece that we could not move before now is dynamic, and we can process its moves.

The Won Bitmaps

The won bitmaps will in general be stored separately from the lost(N) info, so that it can be more or less contiguous on disk. A bitmap for a 4-men chunk will measure 2MB (16M bits representing 64^4 = 16M positions). We will reserve some space between the 2MB bitmaps, though, which we can use to piggyback some other data onto it, which otherwise would have to be gathered separately (requiring extra seek operations). Note that at a transfer speed of 100MB/sec, reading 2MB takes 20 msec, and reading 200KB extra only adds 2 msec to that. A seek operation typically takes 7 msec (due to rotational delay and such), so even if we can save only a single seek by this, it will be a good deal. For reasons that will become apparent later, we will store the won bitmaps for positions only differing in the location of the white King contiguously (except for these 200KB spacers), in the natural square order (a1, b1, ..., h1, a2, b2, ..., g8, h8).

The Won Info for positions differing in the location of another piece than the white King will not be stored contiguously. In stead, it will be alternated with the (much larger) data sets for the lost btm positions for the same set of chunks. Thus, won bitmaps (+spacers) for 64 4-men chunks (in effect forming a 5-men 'super-chunk' of won info) will be followed by 64 set of lost info for the same 64 chunks. This pattern will repeat for every constellation of the white non-King pieces of a 7-men EGT. (Or at least for every canonical representative of each symmetry-equivalent group.) For 6-men EGTs we will also have grouping of the chunks into super-chunks, but due to symmetry requirements the size of the superchunks will be more irregular.

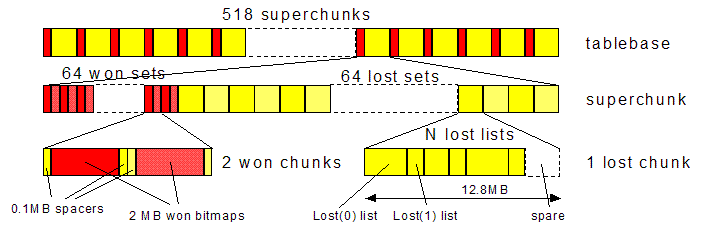
Fig. 1 - Building format of an 8-fold-symmetric 7-men tablebase without exchange symmetry

The Packed Lists of Lost Info

The lost info is more structured: data pertaining to one chunk is subdivided w.r.t. the winning distance. So the packed lists of lost(N) positions for the chunk, N = 0, 1, 2, .., will be concatenated, after padding to make the length an integer number of disk sectors (512 bytes), to facilitate individual writing. The various chunks of lost info will not be contiguous; on the contrary, they will be maximally spaced out to allow the list of lost positions for each chunk to grow maximally by appending new lost(N) info from the next cycle to it, while keeping it contiguous. The lost(N) info will typically be read and written in pairs of winning distances: lost(N) an lost(N+1) together in one contiguous read (for one chunk), and then written back as lost(N+1) and lost(N+2) in a contiguous write after processing.