In the second step, we derive the lost(N+1) positions from the newly-won positions found in the previous step. This is more complicated. The parents of the newly-won positions are not automatically lost(N+1). They are only 'potentially-lost(N+1)', meaning that black has at least one move that loses (namely the one leading to the newly-won position of which it was the parent). But usually black has other moves from this position, and even if there is only one move that leads to a position that is not won (or won in a larger number of moves, so that we do not know it is won yet), then the parent position is not lost(N+1). We thus have to 'verify' the potehtially-lost(N+1) positions (third step), to make sure all black's moves lead to won or newly-won positions.
We thus see that a cycle requires the building of a 3-ply tree: one white unmove, one black unmove, and then a black forward move. The first two levels of this tree have to consider all moves always. The third level can have a cut-off: as soon as we find one black move that saves black, by reaching a position that was not won (for white!), we know the position is not lost(N+1), and we do not have to consider any other black moves.
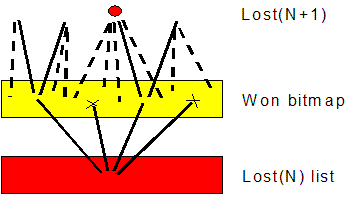
Fig. 4 - Three-ply retrograde tree, folded back onto the same won set. The won info serves both to block branches after ply 1, and to probe for escapes in ply 3.
