Les 2.1 Frequentietabellen en histogrammen

Kranten, bedrijfsrapporten en wetenschappelijke artikelen staan vaak bol van de tabellen en grafieken. Ook in de statistiek maken we hier veel gebruik van. In les 2.2 zal ik een aantal bekende typen tabellen en grafieken behandelen, en in de les daarna hoe verkeerd gebruik van grafieken misleidend kunnen werken. In deze eerste les van Module 2 zal ik laten zien hoe je verzamelde gegevens kunt ordenen in een tabel en deze vervolgens presenteren in een grafiek. Hier voor gebruik ik frequentietabellen en histogrammen. Beide worden veelgebruikt, onder andere in de kansrekening (zie Modules 4 en 5), en dienen als voorbeeld voor het opbouwen van andere tabellen en grafieken.

 Ik zal beginnen met een voorbeeld: Eva, een student aan de plaatselijke universiteit, heeft een universiteits T-shirt ontworpen. Ze wil 1000 T-shirts laten drukken, maar weet niet precies hoeveel van iedere maat. Om een idee te krijgen wat de lengtes zijn van de universiteits studenten neemt ze een steekproef. Ze vraagt a select aan 12 studenten hoe lang ze zijn. Dit zijn de resultaten:

 178 162 191 175 168 186 182 171 179 175 169 170 

 Getallen zoals deze noemen we ruwe gegevens.  Voordat je iets met deze gegevens kan doen, zul je ze eerst moeten ordenen. Je kan dit doen door de studenten in klassen in te delen. De klassen zijn altijd in volgorde. Hier beginnen we met de kortste studenten en eindigen met de langste. Neem bijvoorbeeld vier klassen.

155-165 cm

165-175 cm

175-185 cm

185-195 cm

Turf nu hoeveel studenten er in iedere klasse vallen. Begin met de eerste student. Deze is 178 cm. Deze student hoort dus in de derde klasse thuis. De volgende student is 162 cm lang. Deze hoort in de eerste klasse. Herhaal dit tot je alle studenten hebt afgewerkt.  

Het is belangrijk dat je voor je gaat turven duidelijke afspraken maakt over wat je doet met grensgevallen, dus of studenten van 165 cm in de eerste of tweede klasse vallen. Als je ervoor kiest dat studenten van 165 in de tweede klasse vallen en iedereen die korter is dan 165 cm in de eerste klasse valt moet je een zelfde strategie volgen bij de hogere klassen. Iemand van 175 cm valt dan net in de derde klasse, enzovoort. Je kan ook iets anders afspreken als je maar consequent bent.

 Als je er voor kiest een grensgeval in de hoogste van de twee klassen waar deze precies tussen ligt te latenvallen zal er er 1 student in de eerste klasse vallen, 5 in de tweede, 4 in de derde en 1 in de laatste klasse. Dit is een frequentie tabel voor de lengtes van de 12 studenten  Deze frequentie verdeling gebruiken we om een histogram te ontwerpen. 

Een histogram is een grafiek met op de x-as de klasse indeling en op de y-as frequenties, oftewel de (geturfde) aantallen. Hieronder een histogram dat hoort bij bovenstaande frequentie verdeling.

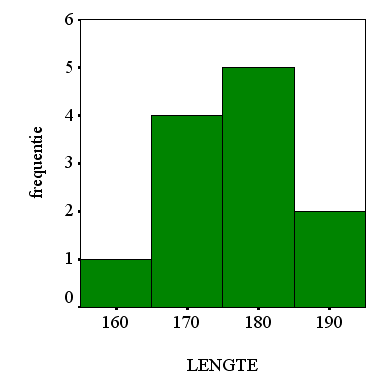
Merk op dat ik in plaats van de klasse breedtes 155-165, 165-175, enzovoort de middens van de respectievelijke klassen (160 cm, 170 cm, enz.) op de assen heb gezet. Dit heb ik gedaan om de grafiek overzichtelijk te houden. Het is ook een gebruikelijke methode om de klassen te benoemen.  Dan spreek je van de klasse rond 160 en 170 cm ipv de eerste en tweede klasse.

Een histogram is dus niets anders dan de grafische weergave van een frequentie tabel. En een frequentie tabel is niets anders dan een indeling van alle gegevens in een aantal van te voren gekozen klassen.

De frequentietabel en met name het histogram maken in een oogopslag duidelijk welke waarden (klassen) veel voorkomen en welke minder. Met andere woorden ze geven een beeld van de verdeling van de waarde stochastische variabele (in ons voorbeeld: lengte).

In plaats van een tabel die aangeeft hoeveel studenten in iedere klasse vallen kunnen we ook een cumulatieve frequentie verdeling weergeven. Een cumulatieve frequentie tabel geeft voor iedere klasse het aantal studenten dat in die klasse vallen plus de aantallen van alle voorgaande klassen. Dus de cumulatieve frequentie voor de eerste klasse is gelijk aan het aantal studenten dat in de eerste klasse valt (1), en de cumulatieve frequentie voor de tweede klasse is gelijk aan het aantal studenten dat in de eerste en tweede klasse samen valt (6), enzovoort.

Onderstaande tabel geeft naast de frequentieverdeling ook de cumulatieve frequentie verdeling voor de eerste twee klassen. Vul zelf de cumulatieve frequenties in voor de laatste twee klassen.

In plaats van een tabel die aangeeft hoeveel studenten in iedere klasse vallen kunnen we ook een relatieve frequentie verdeling weergeven. Een relatieve frequentie tabel geeft voor iedere klasse het percentage lengtes in die klasse, oftewel de frequentie gedeelte door het totaal aantal metingen. In de eerste klasse zit 1 van de 12 studenten dat is 1/12 = 8.33 %. In de tweede klasse zitten 5 van de twaalf studenten dat is 5/12 = 41.67 %

Onderstaande tabel geeft naast de frequentieverdeling ook de relatieve frequentie verdeling voor de eerste twee klassen. Vul zelf de relatieve frequentie in voor de laatste twee klassen in ratio's.  

Merk op dat de vorm van een relatieve histogram exact hetzelfde is als die van een “gewone” histogram. Alleen op de y-as staan nu percentages (in ratios, procenten of decimalen), in plaats van frequenties. Als je de percentages voor alle klassen bij elkaar optelt is dat in iedere relatieve frequentie histogram gelijk aan 1 (of 100 %). In ons voorbeeld: 1/12 + 5/12 + 4/12 + 2/12.

Als je in een gewone histogram de frequenties van alle klassen optelt is dit gelijk aan de totale steekproef grootte. In ons voorbeeld: 1+5+4+2 = 12.

VRAAG:

Dit is een histogram die de relatieve frequenties van het maandelijks bioscoop bezoek van 10 willekeurige mensen weergeeft. Hoeveel van die 10 gaan 2 tot 4 keer per maand naar de bioscoop?

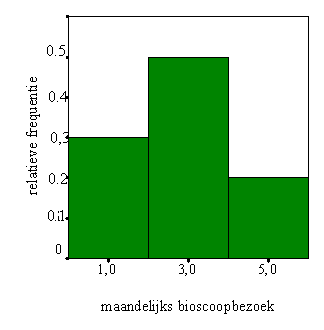
A. 0.5

B. 3

C. 5

 feedback

A 0.5, Nee, de grafiek geeft de relatieve frequentie weer!

B 3, Nee, Het klasse-midden van de klasse van 2 tot 4 is 3, maar dat is niet de frequentie

C 5, Ja, De helft (0.5) van de 10 gevraagde mensen gaan 2 tot 4 keer per maand (klasse-midden 3) naar de bioscoop.

[{plaatje van histogram met 8 staven; x-y combinaties zijn: 110-5, 120-8, 130-5, 140-9, 150-12, 160-7, 170-5, 180-3}