Les 2.2 Regels voor histogrammen

Histogrammen moeten aan een aantal regels voldoen.

Allereerst moet het aantal klassen niet te groot zijn en niet te klein. Sommige tekstboeken geven vuistregels zoals het aantal klassen k moet tussen en in liggen. Of neem als het aantal klassen het eerste gehele getal waarvoor geldt  In beide gevallen wordt met “n” het totaal aantal waarnemingen bedoeld.

Als je het prettig vindt kun je dit soort vuistregels gebruiken. Ik ben er zelf niet zo dol op. Ik vind het belangrijker dat je een beetje gevoel krijgt wat een goed aantal klassen is  in iedere situatie. Je moet altijd in je achterhoofd houden waarom je de histogram maakt. Vaal wil je een idee krijgen over de verdeling van de frequenties over de klassen. Dus je wil graag weten welke waarden veel voor komen en welke weinig.

Als je klasse indeling te klein is geeft dit je vrijwel geen informatie. Als je bijvoorbeeld maar een klasse maakt zitten alle waarnemingen in deze klasse.

Dit geeft je geen extra informatie. In ons voorbeeld wisten we al dat we 12 waarnemingen hadden.

Als je heel veel klassen maakt, ongeveer evenveel als (of zelfs meer dan) er waarnemingen zijn, geeft dit je ook geen informatie, want iedere klasse bevat 0, 1 of misschien hooguit 2 waarnemingen. We wisten al dat er maar 1 student 162 cm was en 1 student 191 en de rest er tussen in.

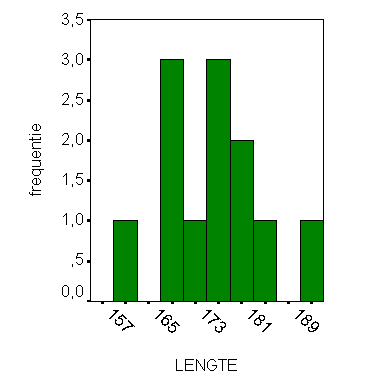
In ons voorbeeld van de lengtes van 12 studenten hebben we gekozen voor 4 klassen, maar 3 klassen of 5 was ook niet slecht geweest. Meer dan 5 of minder dan 3  is naar mijn idee een mindere keuze, maar dit blijft subjectief. Kijk zelf wat je vindt van de verschillende histogrammen met ieder een ander aantal klassen.

Het is natuurlijk zo dat bovenstaande histogrammen van 1, 2, 3 enzovoort klassen maar voorbeelden zijn van histogrammen met 1, 2, 3 enzovoort klassen. Hoe een histogram van een bepaald aantal klassen er precies uitziet wordt mede bepaald door de begin waarde van de eerste klasse, de eindwaarde van de laatste klasse en de klasse breedte.

Welke begin waarde van de eerste klasse en eindwaarde van de laatste klasse je kiest maakt niet zoveel uit zolang de laagste waarde van alle waarnemingen maar in de eerste klasse en de hoogste waarde in de laatste klasse valt.

Het is gebruikelijk om alle intervallen even breed te maken. Dit is niet absoluut noodzakelijk, maar om verwarring te voorkomen wel aan te raden. Vooral als je frequenties in verschillende klassen wil vergelijken is het heel lastig als bv klasse 1 van lage waardes twee keer zo groot is als klasse 2 met hoge waardes.

Het kan dan lijken bij frequentie van bijvoorbeeld 16 in klasse 1 en een frequentie 10 in klasse 2 dat lage waardes meer voorkomen dan hoge waardes. Echter als we van klasse 1 twee klassen ter grootte van klasse 2 hadden gemaakt hadden die ieder maar 8 elementen, of een 7 en de ander 9 elementen kunnen hebben. Dan zouden we correct hebben geconcludeerd dat hoge waardes iets meer voorkomen dan lage en midden waardes.Wees dus heel voorzichtig als je niet alle klassen even breed maakt. In hetgeen dat volgt ga ik er vanuit dat alle klassen even breed zijn.

De klassenbreedte wordt bepaald door de begin en eindwaarde en het aantal klassen dat je wilt maken:

Klassenbreedte = (eindwaarde-beginwaarde)/(aantal klassen)

Omgekeerd, het aantal klassen wordt bepaald door de klasse breedte en de begin en eindwaarde:

Aantal klassen =  (eindwaarde-beginwaarde)/(klassenbreedte)

Bij het kiezen van begin en eindwaarde zowel als de klassenbreedte zou ik als advies willen geven: Zorg altijd dat de klassenbreedte een mooi interval is. In ons voorbeeld hebben we klassen genomen van 10 cm. Dat is een mooie en makkelijke maat. We hadden ook 4 klassen kunnen maken van 11,34 cm maar dat is niet mooi, niet handig, en er is ook geen enkele reden toe.

[figuur F5-11]

 Dus, probeer altijd klassen van 5, 10, 100 of dergelijke eenheden te maken, dat werkt veel makkelijker dan intervallen van bijvoorbeeld 56,8376. In iets mindere mate geldt iets soortgelijks ook voor de begin en eindwaarde. Het is eenvoudiger werken met een beginwaarde van 155, in plaats van 155,343.

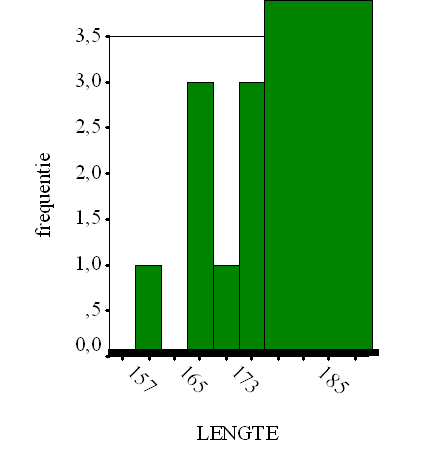
Als laatste zou ik willen opmerken dat je moet zorgen dat alle klassen aansluiten en niet overlappen. Op deze manier zorg je ervoor dat alle waarnemingen in precies een klasse terecht komen en niet meer of minder dan 1 keer geteld worden.

[Figuur 5-12]

In de figuur hierna wordt de lengte 168 cm niet geteld en 178 cm twee maal. Dit geeft natuurlijk een erg verdraaid beeld.

HIER MENSEN HUN EIGEN LENGTE IN LATEN TYPEN? OF TOCH ERGENS ANDERS?

VRAAG:

Wat is de klasse breedte in het volgende histogram?

A 8, Nee, dit is het aantal klassen.

B 8.75, Nee, kijk nog eens goed naar het histogram, met name de x-as.

C 10, Ja, het verschil tussen de klassenmiddes is steeds 10.

[{plaatje van histogram met 8 staven; x-y combinaties zijn: 110-5, 120-8, 130-5, 140-9, 150-12, 160-7, 170-5, 180-3}