Les
1.2, Steekproeven en populatie
Het
begrip “populatie” binnen de statistiek is breder dan een groep mensen die
in een land wonen. In het algemeen spreken we van een gehele verzameling
elementen. Deze elementen kunnen mensen zijn, of dieren, of dingen of
gebeurtenissen die je wilt onderzoeken. Dus een populatie kan alle inwoners van
een land zijn, maar ook alle mussen in een park, alle chocolade repen
geproduceerd in een fabriek, of zelfs alle operaties in een ziekenhuis in een
jaar. Essentieel is dat het om een groep elementen gaat waar onderzoek naar
uitgaat.
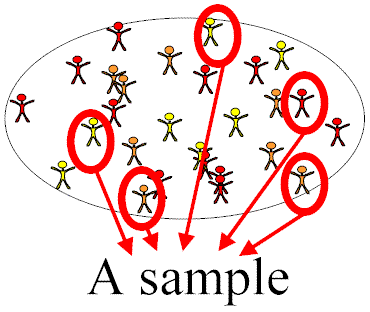
Een
steekproef is een deelverzameling van de populatie. Een steekproef wordt genomen
om zonder de hele populatie te bekijken iets te zeggen over deze populatie.
Vraag
In
een biologisch onderzoek wordt de staat van de Drentse hei bekeken. Wat is in
dit soort onderzoek de heide?
a)
Een
verzameling
b)
Een
populatie
c)
Een
steekproef
Antwoord
a)
Nee
b)
Ja
c)
Nee
De
bedoeling van een steekproef is om zo veel mogelijk informatie over een
populatie te krijgen met zo min mogelijk metingen. Meestal worden steekproeven
dan ook genomen om tijd en geld te sparen.
Als
men vlak voor de verkiezingen een idee wil krijgen over hoe Nederlanders zullen
stemmen dan is het veel te omslachtig en veel te duur om iedere stemgerechtigde
alvast te vragen wat hij of zij denkt te gaan stemmen. Het is veel goedkoper en
sneller om een peiling uit te voeren bij een gedeelte van alle stemgerechtigden.
Soms
worden steekproeven uitgevoerd omdat het fysiek onmogelijk is om een hele
populatie te meten. Het is bijvoorbeeld onmogelijk om alle vissen in de zee te
tellen.
(gekleurde
vissen zwemmen voorbij)
Een
andere situatie is waar de populatie oneindig is. Het gooien van een dobbelsteen
kan oneindig vaak gebeuren. Om een idee te krijgen of alle zijden even vaak
boven komen, en zo niet welke zijden vaker boven komen kan je een steekproef
nemen door de dobbelsteen bijvoorbeeld 100 keer te gooien.
(Dobbelsteen,
met steeds een andere kant boven)
Een
andere goede reden voor een steekproef ontstaat wanneer hetgeen je wilt meten
kapot gaat door de meting. Als je in een touwfabriek wilt testen bij welke
kracht een bepaald type touw knapt is het niet handig om aan al het
geproduceerde touw steeds harder te trekken tot het knapt. Je weet dan bij welke
kracht het touw knapt maar je hebt geen touw meer over. Voer je de krachttest
echter uit op een steekproef uit al het geproduceerde touw, dan kun je de kracht
schatten waarbij dit type touw gemiddeld knapt.
(Touw
waar steeds harder aan wordt getrokken en dat uiteindelijk knapt)
Naast
dit alles, vermindert het gebruik van steekproeven het aantal meetfouten. In een
steekproef worden minder metingen gedaan dan in een populatie. Dan kunnen er ook
minder fouten gemaakt worden.
Een
steekproef kan alleen goede en voldoende informatie over een populatie geven,
als de steekproef representatief voor de populatie is. Wat is een
representatieve steekproef denk je?
Als
we het kiesgedrag van Nederlanders willen peilen ben jij dan een representatieve
steekproef?
(tekening
van een groep mensen. Een grote hand boven de mensen wijst een mensje aan. Deze
kijkt een beetje angstig)
Nee,
ik vrees het niet. Als jij samen met nog 999 anderen was uitgekozen dan was het
een ander verhaal, maar een persoon is niet genoeg. Als jij PvdA stemt zegt dat
nog helemaal niets over de rest van de bevolking. Een steekproef van een
persoon, of twee of zelfs vijf of tien is veel te klein. Hoe groter de
steekproef hoe beter beeld je krijgt. Aan de andere kant hoe kleiner de
steekproef hoe sneller en goedkoper. Het is altijd de kunst om een goed
evenwicht te vinden tussen deze twee tegenwerkende krachten.
Wat
denk je, is een schoolklas een representatieve steekproef?
(tekening
schoolklas)
In
eerste instantie is een schoolklas waarschijnlijk te klein. Veel belangrijker is
dat je niet trekt uit de doelpopulatie trekt. Je doel populatie is niet
Nederlanders, maar stemgerechtigde Nederlanders. Daar meeste schoolkinderen
onder de 18 zijn, zal een steekproef van schoolkinderen geen informatie geven
over het kiesgedrag van stemgerechtigde Nederlanders.
Nou,
wat denk je van alle volwassen bezoekers aan een golfveld op een dag? (tekening)
In
Nederland is golf redelijk een elite sport. Waarschijnlijk geeft het stemgedrag
van de bezoekers aan het golfveld daarom een scheef beeld. Het is heel
belangrijk dat als je een steekproef neemt je niet een heel specifieke groep
uitkiest maar je de steekproef zo willekeurig mogelijk neemt, dus zoveel
mogelijk door het toeval laten bepalen. Je kiest bijvoorbeeld 100 willekeurige
stemgerechtigde Nederlanders uit het bevolkingsregister van 10 willekeurig
gekozen gemeentes. In statistische termen zeggen we dat een steekproef aselect
moet zijn. Dat wil zeggen: louter door het toeval bepaald en dus geheel
willekeurig.
De
meest pure manier om een willekeurige, oftewel aselecte, steekproef te nemen is
met behulp van zogenaamde aselecte cijfer tabellen. De engelse term hiervoor,
random number tables, wordt ook vaak gebruikt.
De
aselecte cijfer tabellen zijn overzichten van volledig willekeurige getallen die
bijvoorbeeld in kolommen van 5 cijfers worden weergegeven zoals in Tabel 1.1
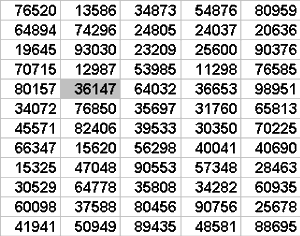
Voor
je de tabel kan gebruiken moet je de gehele populatie waar je de steekproef uit
wilt trekken nummeren. Dus in het geval van de Nederlandse stemgerechtigde
bevolking krijgt iedereen een nummer van 1 tot 12 miljoen, of wat dan ook het
exacte aantal stemgerechtigde Nederlanders is.
Om
het voorbeeld niet te ingewikkeld te maken ga ik er nu even van uit dat de
populatie alleen de 800 stemgerechtigde inwoners van een dorp betreft. Dus je
wilt met behulp van een aselecte cijfer tabel een aselecte steekproef van
bijvoorbeeld 20 dorpelingen trekken om daarmee een idee van het stemgedrag van
het dorp te krijgen.
Nummer
alle 800 inwoners. Kies dan op een willekeurige plaats in de tabel het eerste
aselecte getal. Je kan bijvoorbeeld je ogen dicht doen en gewoon prikken, maar
je kan bijvoorbeeld ook als je verjaardag 2 mei is het getal in de tweede kolom
en de vijfde rij kiezen.
(Door
een druk op een knop, of andere manier moet deze plaats inde tabel nu oplichten).
Voor
je verder gaat kiezen moet je eerst een aantal besluiten nemen. Allereerst is
het nummer van ieder van de 800 inwoners maximaal 3 cijfers groot. Het heeft dus
geen zin om alle vijf de cijfers uit een kolom te gebruiken. Je moet van tevoren
beslissen of je steeds de eerste drie, de laatste drie of een andere combinatie
van drie uit vijf gebruikt. Daarnaast moet je beslissen hoe je verder gaat nadat
je het eerste aselecte getal hebt getrokken. Ga je inde tabel naar beneden, of
naar boven, of naar links of rechts? Neem je steeds het volgende getal, of sla
je één of twee getallen over?
Stel
je kiest voor de eerste drie van de vijf cijfers. Voor ieder volgend getal ga je
naar beneden, en sla je iedere keer één rij over. Als je aan het eind van de
kolom komt, ga je verder met de kolom die er rechts naast ligt.
(In
een simulatie (met of zonder op knoppen drukken) laat zien wat de
achtereenvolgende getallen zijn. Als een getal groter is dan 800 verschijnt er
een kruis door het getal met de tekst)
Een
aselect getal dat groter is dat de populatie, in dit geval 800, moet
overgeslagen worden. Niemand heeft dit nummer.
Deze
procedure kun je ook uit voeren met een steekproef van 1000 uit de 12 miljoen
stemgerechtigde Nederlanders. Het is dan wel veel handiger om gebruik te maken
van een zogenaamd aselecte cijfer generator (eng: random number generator). Dit
is een computer programma dat aselecte cijfers uitspuwt op basis van een
populatie- en steekproef-grootte die jij op geeft. Op het Internet zijn er vele
te vinden. Ik heb er hier ook één toegevoegd.
Hier een random generator applet plaatsen, met wat aanwijzingen en oefeningen om het uitte proberen.
Probeer
maar eens een steekproef van 5 uit een populatie van 12 miljoen te trekken. Let
er daarbij op dat alle getrokken nummers tussen de 0 en 12 miljoen moeten
liggen.
Nog
even terugkomend op de aselecte cijfer tabellen: Deze kunnen efficiënter
gebruikt worden als de nummering van de elementen in de populatie volstrekt
willekeurig is. Dus als inwoners niet op basis van bijvoorbeeld leeftijd of
woonwijk zijn genummerd, maar volstrekt willekeurig. Je kan dan een
systematische aselecte steekproef trekken in plaats van een gewone aselecte
steekproef. In dat geval hoef je slechts één aselect cijfer te trekken. Dit
kan doordat je de populatie opdeelt in net zoveel groepen als de steekproef
groot is. Iedere groep bevat evenveel nummers, namelijk de populatiegrootte
gedeeld door de steekproefgrootte Dus in het dorp bevat de eerste groep de
inwoners met nummers 1 tot 800/20 = 40. de volgende groep bevat de volgende 40
inwoners. Dat zijn de inwoners met nummer 41 tot 80, enzovoort. Met behulp van
een aselecte cijfer tabel (of eventueel generator) trek je een aselect getal
tussen 1 en 40. Dit is bijvoorbeeld 24. Je steekproef van 20 bestaat dan uit de
inwoners met nummers 24, 24 +40 =64, 24+40+40=104, enzovoort tot en met nummer
784.

Naast
de normale aselecte steekproef en de systematische aselecte steekproef bestaan
er nog vele andere vormen van min of meer aselecte steekproeven. Ik zal er hier
een paar bespreken.
Allereerst
is er de gelede steekproef. Deze wordt gebruikt als er duidelijke verschillen
zijn tussen bepaalde groepen in de populatie. Sommige bevolkingsgroepen vertonen
een duidelijk ander stemgedrag dan andere bevolkingsgroepen. Jongeren stemmen
anders dan ouderen en die stemmen weer anders dan mensen met een leeftijd tussen
die van jongeren en ouderen. Ook gelovigen stemmen vaak anders dan niet
gelovigen. Om een goed beeld van de hele populatie te krijgen moet je zorgen dat
de samenstelling van de steekproef ten aanzien van de bevolkingsgroepen min of
meer overeenkomt met de werkelijke samenstelling. Met andere woorden als de ene
bevolkingsgroep 30% van de populatie betreft en de andere 70%, moet je er voor
zorgen je steekproef ook ongeveer deze verhouding heeft. Oftewel selecteer 30%
van je steekproef uit de eerste groep en 70% van je steekproef uit de tweede
groep. In een gelde steekproef bepaal je per groep het stemgedrag.
Naast
de gelede steekproef kennen we ook de cluster steekproef. Hierbij is het de
onderzoeker die de populatie in groepen opdeelt in plaats van dat er al
duidelijk groepen zijn. Een bekende methode is het land opdelen in vele kleine
geografische gebieden. Selecteer uit deze gebieden een aantal representatieve
gebieden en ondervraag alle inwoners in die uitgekozen gebieden.
Plaatje
land indelen in groepen. Een paar van de gebieden worden als geheel gekleurd
Een
variant op de cluster steekproef is de meerstadia steekproef. Hierbij wordt de
populatie niet alleen in groepen opgedeeld maar worden aselecte steekproeven
genomen in een paar van de aselect gekozen groepen. Dus alleen een paar mensen
die in de gekozen gebieden wonen worden ondervraagd.
Zelfde
plaatje als net maat nu zie je een paar gekleurde stipjes in de paar gebieden
die net nog geheel gekleurd waren.
Vraag
80 ziekenhuizen zijn betrokken bij een onderzoek naar het effect van een nieuw medicijn tegen te hoge bloeddruk. In een eerste vooronderzoek krijgen 10 patiënten in 8 ziekenhuizen het medicijn. Hoe zou je dit type steekproef noemen?
a) Gelede steekproef
b) Cluster steekproef
c) Meerstadia steekproef
Antwoord
a) nee
b) nee
c) ja
Hoe
je een steekproef neemt hangt af van wat voor soort onderzoek je doet. Dat wil
zeggen in welk vakgebied je onderzoek doet, wat je budget is, wat je doel is en
daaruit voortvloeiend wat je hypotheses zijn en vraagstelling.
Iemand
die experimenteel onderzoek doet naar een scheikundig verschijnsel doet een heel
ander type onderzoek dan iemand die het gedrag van mensen bestudeert. Binnen de
laatste categorie is er weer een wereld van verschil tussen de psycholoog die
wetenschappelijk onderzoek doet naar bijvoorbeeld het kopieergedrag in groepen
en een student die als onderdeel van zijn studie het gedrag van medestudenten
tijdens feestjes bestudeert. De eerste zal een veel grootschaliger onderzoek
doen met een ruimer budget. Het budget bepaald ook hoeveel mensen men kan
bestuderen, oftewel hoe groot de steekproef is.
Afhankelijk
van de aard van het onderzoek moet gekeken worden of er een experimenteel
onderzoek of een observerend onderzoek wordt opgezet. De scheikundige zal
waarschijnlijk een experimenteel onderzoek doen waarbij hij van tevoren een
statistische proefopzet maakt. Binnen zo’n proefopzet zal hij proberen zoveel
mogelijk variabelen te controleren zodat hij zeker is van wat en hoe het
verschijnsel verklaard kan worden. De statistiek achter het proefopzetten is een
vak apart en wordt onder andere in Module... in meer detail behandeld.
Menselijke
gedragingen daarentegen worden vaak onderzocht met behulp van observaties. Ook
kunnen daarbij vragenlijsten gebruikt worden. Dit brengt weer een heel eigen
manier van steekproef trekken met zich mee. Bij vragenlijsten heb je
bijvoorbeeld het probleem van de non-reponse.
Niet iedereen die je een vragenlijst opstuurt zal deze invullen. De vraag
daarbij is of de groep mensen die de vragenlijst invult representatief is voor
de hele populatie. Als voornamelijk plichtsgetrouwe mensen de lijst invullen en
opsturen en het onderzoek betreft iets waarbij er duidelijke verschillen zijn
tussen plichtsgetrouwe en minder plichtsgetrouwe mensen is er waarschijnlijk
sprake van een zekere mate van afwijking. Ook kan er een afwijking ontstaan als
je een uitspraak wilt doen over de gehele bevolking van een land en je
onderzoekt als student alleen je mede studenten (steekproef selectie afwijking). De meningen van je medestudenten
zijn niet representatief voor de gehele bevolking omdat je waarschijnlijk een
select gezelschap hebt qua leeftijd, opleiding en interesse. Daarnaast kunnen
nog afwijkingen ontstaan indien een interviewer de vragen stelt en dit niet
neutraal doet (vraagsteller afwijking)
of de vragen gevoelig zijn en men de neiging heeft sociaal wenselijk te
antwoorden of in ieder geval jezelf niet in een negatief daglicht wil zetten (eigenbehoud
afwijking)
Al
met al moge het duidelijk zijn dat er veel typen steekproeven zijn die
afhankelijk van het soort onderzoek het best gekozen kunnen worden, maar die
ieder ook hun eigen problemen met zich mee brengen. Dit is niet de plaats om
hier nu verder in detail op in te gaan. Gedurende de cursus zal je met de meeste
veelgebruikte typen steekproef in aanraking komen en steeds beter een gevoel
krijgen wat je in welke situatie het beste kan gebruiken. Het belangrijkste
daarbij is dat je er altijd naar streeft dat je steekproef representatief is,
dus a select en voldoende groot.
Vraag
Een
jonge man is gevraagd in een winkelstraat een korte vragenlijst af te nemen over
het gebruik van SMS. Om zijn werk te veraangenamen ondervraagt hij alleen
meisjes die hij er leuk vindt uitzien. Tot wat voor soort afwijking in de
steekproef kan dit leiden?
a)
Eigenbehoud
afwijking
b)
Vraagsteller
afwijking
c)
Steekproef
selectie afwijking
Antwoord
a)
Nee,
het gaat hierbij met name om de keuze van personen die de jonge man ondervraagt.
b)
Nee,
het gaat hierbij met name om de keuze van personen die de jonge man ondervraagt.
c)
Ja,
De groep die hij ondervraagd is vanwege het feit dat het slechts één geslacht
betreft en een beperkte leeftijdsgroep, en waarschijnlijk ook een bepaalde
interesse groep niet representatief voor de gehele bevolking.