Numerieke wiskunde XVII:
Integreren met de Trapeziumregel
 Stel: je wilt de oppervlakte
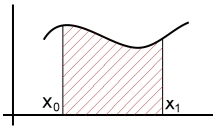
berekenen onder de grafiek van een functie. Zie de figuur hiernaast. De oppervlakte die we zoeken is gearceerd.
Stel: je wilt de oppervlakte
berekenen onder de grafiek van een functie. Zie de figuur hiernaast. De oppervlakte die we zoeken is gearceerd.
Het domein (dat is de waarde van x) loopt van x0 tot x1.
Bij een wat meer ingewikkeld functievoorschrift is analytisch integreren meestal lastig (lees: moeilijk). Numeriek Integreren
is dan een mogelijke oplossing.
Op deze pagina gaat het over de trapeziumregel.
 Het domein wordt verdeeld in een eindig aantal stapjes. Uit de functiewaarden aan het begin en eind van elke stap, en de
stapgrootte
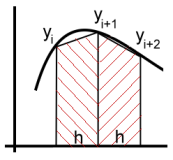
Het domein wordt verdeeld in een eindig aantal stapjes. Uit de functiewaarden aan het begin en eind van elke stap, en de
stapgrootte h, wordt het oppervlak van een trapezium berekend (de functiewaarden worden verbonden door rechte lijnen). De som van alle 'plakjes oppervlak' is een benadering van de totale oppervlakte onder de grafiek.- Hierbij geldt: Hoe kleiner de stap
h, hoe nauwkeuriger de oplossing.
- De oppervlakte van één plakje is gelijk aan:
a = ½(yi + yi+1) · h. - Het totale oppervlak is dan:
A = ∑ (a) = ∑ ½(yi + yi+1) · h, waarbijiloopt van0tot en metn-1.
- De stapgrootte
hhoeft tijdens het rekenproces niet constant te zijn. Het is in principe mogelijk omhtijdens het rekenproces te vergroten of te verkleinen, afhankelijk van het verloop van de functie. - Een eenvoudiger aanpak is door de berekening meerdere maken uit te voeren, met kleinere, constante, stapgrootte en de opeenvolgende resultaten te vergelijken. De resultaten zullen steeds minder verschillen. Als de verschillen klein genoeg zijn, heb je een behoorlijke benadering van de oppervlakte. Maar het is nog steeds een benadering!
Een uitgewerkt voorbeeld
Vraag: Wat is het oppervlak onder de grafiek van y = sin(x) tussen x0 = 0°
en x1 = 180°?
Uitwerking: In de meeste (alle?) computertalen rekent de ingebouwde sinus-functie in radialen. Het is
daarom het handigste om de integraal uit te rekenen van x0 = 0 tot x1 = π
 Als eerste
tekenen we de grafiek van
Als eerste
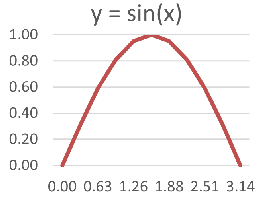
tekenen we de grafiek van y = sin(x)tussenenπ, zie de figuur hiernaast.- Om het voorbeeld wat overzichtelijk te houden lossen we dit op 10 stappen, dus
n = 10.y = sin(x)wordt dus berekend voorx = 0; π/10; 2π/10; 3π/10; .... π;/, in totaal dus 11 keer. Zie onderstaande tabel. - De grafiek van
sin(x)verloopt glad over het hele domein. De figuur is gebaseerd op de tabel hieronder, waarbij de elf punten zijn verbonden door rechte lijnen. Dat is vooral goed te zien rondx = π/2. Het is een indicatie dat de fouten in de benadering daar het grootste zijn.
| i | x | y | a | |||
| 0 | 0.00000 | 0.00000 | 0.048540 |
|||
| 1 | 0.31416 | 0.30902 | 0.140869 |
|||
| 2 | 0.62832 | 0.58779 | 0.219409 |
|||
| 3 | 0.94248 | 0.80902 | 0.276472 |
|||
| 4 | 1.25664 | 0.95106 | 0.306471 |
|||
| 5 | 1.57080 | 1.00000 | 0.306471 |
|||
| 6 | 1.88496 | 0.95106 | 0.276472 |
|||
| 7 | 2.19911 | 0.80902 | 0.219409 |
|||
| 8 | 2.51327 | 0.58779 | 0.140869 |
|||
| 9 | 2.82743 | 0.30902 | 0.048540 |
|||
| 10 | 3.14159 | 0.00000 | ||||
A = ∑ (a) = | 1.983523 |
|||||
- De exacte oplossing van
∫ sin(x)dxtussen0enπis gelijk aan 2. De afwijking wordt voornamelijk veroorzaakt door de onnauwkeurigheid rondπ/2. - Als je de berekening uitvoert met 100 stappen in plaats van 10, wordt de uitkomst gelijk aan 1.9998355. Dat
lijkt al meer op de exacte oplossing.
Omdat de trapeziumregel een benaderingsmethode is, wordt de exacte oplossing nooit gehaald.
Met 1000 stappen wordt de uitkomst 1.999998355.
 Natuurlijk is er ook een applicatie om zelf met deze techniek
aan de slag te gaan. Klik op de knop hiernaast.
Natuurlijk is er ook een applicatie om zelf met deze techniek
aan de slag te gaan. Klik op de knop hiernaast.- De applicatie berekent de stapgrootte uit de integratiegrenzen en het aantal stappen. Dat is constant gedurende de berekening.
- De applicatie toont alle beschikbare decimalen in de uitkomst. Er wordt dus niet afgerond!
- De code van de applicatie kun je downloaden om zelf aan door te ontwikkelen.
- Als je verder wilt werken aan de applicatie, download je de .zip-file en pak je hem uit. Je hebt dan meteen een werkend voorbeeld.
Downloaden:
Druk op de knop:
![]() File: voorb667.zip, 3253 bytes.
File: voorb667.zip, 3253 bytes.
