Het uitwerken van natuurkundige opgaven
Wat kan er zoal misgaan bij het uitwerken van opgaven, diagnostische toetsen, repetities en examens? Haal je voordeel uit het volgende overzicht.
De leerling... |
||
| • vermeldt in een formule eenheden in plaats van grootheden; | Een onjuiste formule is bijvoorbeeld: snelheid = meter / seconde of, in symbolen: v = m / s In plaats van de eenheden meter en seconde horen er de grootheden afstand en tijd te staan, of hun symbolen s en t. Hieronder zie je enkele goede mogelijkheden. snelheid = afstand / tijd snelheid = verplaatsing / tijdsduur v = s / t v = Δx / Δt |
|
| • slaat in een berekening het opschrijven van een formule in symbolen over; | Voor het berekenen van de gemiddelde snelheid van een dier dat zich in een tijdsduur van 2,2 seconde over een afstand van 6,5 meter weet te verplaatsen mag je schrijven: s = v · t 6,5 = v · 2,2 waaruit volgt dat v = 3,0 m/s Laat je de eerste regel weg dan is je uitwerking niet compleet. |
|
| • schrijft in een berekening de formule met ingevulde getallen niet op; | Voorbeeld: de ingevulde formule 6,5 = v · 2,2 of (6,5 m) = v · (2,2 s) mag in de uitwerking niet ontbreken. Laat telkens zien welke waarden je invult. Vul formules dus altijd één op één in. |
|
| • geeft een einduitkomst zonder een eenheid; | De lengte is 17. Wie dat schrijft zegt niets. Is de lengte 17 mm, 17 cm of 17 km? Wellicht 17 inch? We weten het niet; zonder eenheid blijft de bedoelde lengte onbekend. Van een berekende snelheid v = s / t = 6,5 / 2,2 = 2,95 = 3,0 word je ook niet veel wijzer zolang je niet weet of 't gaat om m/s, km/h, cm/min, km/s of welke andere eenheid voor snelheid dan ook. |
|
| • laat de eenheid in een tussenuitkomst weg; | Ook een tussentijds berekende grootheid is alleen duidelijk als zowel het getal als de eenheid vermeld zijn. grootheid = getal (×) eenheid Het vermenigvuldigingsteken wordt gewoonlijk weggelaten: tijdsduur = 47 seconde. |
|
| • geeft een einduitkomst met een onjuiste significantie; | Door aanwezigheid van meetonzekerheden is de waarde van een grootheid nooit exact bekend. Daarom wordt de uitkomst van een berekening met meetwaarden afgerond op het aantal significante cijfers dat past bij de nauwkeurigheid van de meetwaarden. Bijvoorbeeld: v = s / t = 6,5 / 2,2 = 2,9545 = 3,0 m/s (uitkomst in 2 significante cijfers). De uitkomsten 2,95 m/s (3 significante cijfers) en 3 m/s (1 significant cijfer) voldoen niet omdat ze niet in overeenstemming zijn met de nauwkeurigheid van de meetwaarden 6,5 m en 2,2 s. |
|
| • rondt de einduitkomst niet goed af; | Rond in het gegeven voorbeeld niet zo af v = 2,95 = 2,9 m/s maar zo v = 2,95 = 3,0 m/s. |
|
| • rekent verder met een afgeronde uitkomst; | Reken verder met tenminste één cijfer méér dan nodig is in de einduitkomst van een opgave. Als de snelheid v niet de einduitkomst van de opgave is, maar slechts een tussenuitkomst, dan reken je dus niet met 3,0 m/s maar met 2,95 m/s of 2,955 m/s verder. Nog beter: sla het getal 2,9545... op in geheugen X van je rekenautomaat. Met maar één tik (op de X-toets) roep je het getal later weer op. (Met geheugen X werk je sneller dan met geheugens A, B, enz.)   Met een druk op de toetsen [STO] en [X] sla je het laatste rekenresultaat op in geheugen X. Toets je daarna bijvoorbeeld [3], [X] en [ENTER] dan verschijnt meteen het drievoud van het opgeslagen getal. |
|
| • gebruikt een ongeldige formule; | Bijvoorbeeld: s = v · t geldt alleen maar als de snelheid in het bekeken tijdsinterval constant is. Voor een beweging waarbij de snelheid van het voorwerp niet verandert is de formule dus zonder bezwaar te gebruiken. Als de snelheid wél verandert mag alleen de gemiddelde snelheid in het tijdsinterval ingevuld worden en niet een snelheid op een willekeurig tijdstip. Omgekeerd, bij invulling van een verplaatsing en een tijdsduur vind je de gemiddelde snelheid van het voorwerp in de bekeken tijdsduur. Werken met de schrijfwijze s = vgem · t verkleint de kans op onjuiste toepassing van de formule. |
|
| • maakt een rekenfout; | Tja... doe 't niet te vaak. |
|
| • geeft een onvolledige uitwerking; | De uitleg, berekening of bepaling is dan niet compleet. In een redenering mogen essentiële 'schakels' of logische stappen niet ontbreken. | |
| • geeft een goede uitkomst zonder een gevraagde berekening of bepaling. | (Levert doorgaans nul punten op.) | |
Werken met formules1 - Schrijf de formule op in symbolen van grootheden (s = v · t); 2 - Vul de waarden van alle bekende grootheden één op één in (6,5 = v · 2,2); 3 - Reken de onbekende resterende grootheid uit (v = 2,955 = 3,0 m/s). |
||
De leerling... |
||
| • gebruikt een grootheid die niet in de juiste eenheid is omgerekend; | Voorbeeld. Een versnelling a wordt gewoonlijk uitgedrukt in de eenheid m/s2 (meter per seconde kwadraat). Bij gebruik van de formule a = Δv / Δt moet je daarom een snelheidsverandering Δv die gegeven is in km/h, eerst omrekenen naar de eenheid m/s voordat je de deling uitvoert. | |
| • schrijft onzin op zoals: 3 + 1 = 4 × 2 = 8; |
Het eerste =-teken is niet toegestaan, want 4 ≠ 8. Voer beide berekeningen gescheiden uit: 3 + 1 = 4 4 × 2 = 8, of schrijf de vergelijking zelf goed op: (3 + 1) × 2 = 4 × 2 = 8. |
|
| • schrijft onzin op zoals: 5,0 kg = 49 N 2,0 L = 2,0 kg; |
Een massa is nooit gelijk aan 'n kracht. En een volume kan onmogelijk gelijk zijn aan een massa. Uit een gegeven massa kan wel volgen hoe groot de zwaartekracht is die erop werkt, dus: m = 5,0 kg ⇒ F = 49 N. Een andere goede weergave is: 5,0 kg 'komt overeen met' 49 N, wat kort genoteerd mag worden als: 5,0 kg Een bepaald volume van een stof (water) kan iets zeggen over de massa: V = 2,0 L ⇒ m = 2,0 kg. |
|
Diagrammen, grafieken |
||
| • past in de assen van een diagram een 'zaagtandlijn' of 'scheurlijn' onterecht of niet juist toe; | Het gebruik van een 'zaagtand' kan nadelig zijn. Je ziet bijvoorbeeld niet meer of de grafieklijn door de oorsprong gaat. | |
| • verwisselt in een diagram de twee grootheden die langs de assen moeten worden uitgezet; | De drie mededelingen (1) "Teken een (v,t)–diagram" (2) "Zet de snelheid in een diagram uit tegen de tijd" (3) "Teken de snelheid als functie van de tijd in een grafiek" betekenen (in de natuurkunde) alle dat de snelheid verticaal en de tijd horizontaal moet worden uitgezet. Opmerking Het ligt voor de hand om de onafhankelijke grootheid (de oorzaak) langs de horizontale as en de afhankelijke grootheid (het gevolg) langs de verticale as uit te zetten. Toch wordt daar soms van afgeweken, zoals in een (U,I)–diagram. Hoewel de elektrische spanning U (in volt) de 'drijvende kracht' (de oorzaak) is achter het lopen van een stroom en de stroomsterkte I (in ampère) dus het gevolg, wordt hier U tegen I uitgezet. |
|
| • vermeldt niet alle grootheden en eenheden langs de assen van een diagram; | Langs de horizontale as zou bijvoorbeeld kunnen staan:
tijd (seconde) → of korter t (s) →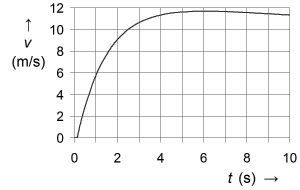 Een topatleet trekt een 100-meter-sprint. |
|
| • gebruikt langs een as van een diagram geen goede verdeling van maatstrepen; | Gebruik bij voorkeur veelvouden van 1, 2 of 5 en vermenigvuldig waar nodig met een macht van tien. Voorbeelden: 0 1 2 3 enz; 0 2 4 6 enz; 0 5 10 15 enz; 0 20 40 60 enz; 0 0,05 0,10 0,15 0,20 enz. Je mag de macht van tien ook bij de eenheid vermelden. Het laatste geval wordt dan: 0 5 10 15 20 enz. met langs de as: v (10–2 m/s) → In plaats van de macht van tien voor de eenheid mag je ook een geschikt voorvoegsel gebruiken: 0 5 10 15 20 enz. v (cm/s) → In dit voorbeeld is het getal 100 maal zo groot gemaakt. Dan moet de eenheid 100 maal zo klein worden om de grootheid onveranderd te houden. Dat volgt uit: grootheid = getal × eenheid. |
|
| • vermeldt te veel of te weing getallen langs een as van een diagram; | Houd het diagram overzichtelijk en goed afleesbaar. | |
| • tekent een meetpunt op een verkeerde plaats in een diagram; | Vooral bij een beperkt aantal punten kan een onjuist ingetekend meetpunt het vinden van de goede (meest waarschijnlijke) grafieklijn in de weg staan. | |
| • maakt een grafieklijn door opeenvolgende meetpunten te verbinden (tot bijvoorbeeld een zigzaglijn); | De natuur trekt zich weinig aan van gemaakte meetfouten. | |
| • laat bij het bepalen van de grafieklijn sommige meetpunten zwaarder meetellen dan andere; | Het eerste en vooral het laatste meetpunt van een reeks lijken wel eens een 'magische' invloed op de ligging van de grafieklijn te hebben. In beginsel zijn alle meetpunten even waardevol. |
|
| • tekent een grafieklijn niet voldoende zorgvuldig. | Teken een dunne lijn. Een lijn die niet kaarsrecht is, is geen rechte lijn. Een vloeiende kromme is strak, niet hoekig. | |
| En verder:
Gebruik in uitwerkingen geen rode inkt en ook geen potlood. Gebruik in getallen niet de punt, maar de komma als decimaal scheidingsteken. Corrigeer je uitwerkingen van diagnostische toetsen met rode inkt en markeer de fouten duidelijk. Bestudeer deze fouten nogmaals vlak voor het maken van een repetitie of 'n andere toets. Reken je niet rijk bij de correctie van gemaakte diagnostische toetsen. Voorbeeld: een onjuiste eenheid in een tussenuitkomst of in de einduitkomst kost je één punt. Let ook op de significantie in de einduitkomst.
Voor meer weetjes over het werken met grootheden en eenheden, getallen, SI-eenheden, onzekerheid en significante cijfers ga je naar deze tips voor natuurwetenschappelijke verslaglegging. |
Hein ten Horn
![]() Top | Physics | Home
Top | Physics | Home