Berthe en haar interesses
wiskunde is kunst DE GULDEN SNEDE |
Heb je weleens ontdekt dat vier gelijkzijdige driehoeken
een vierkanten basis kunnen geven
en wist je dat dat de constructie is van een van een pyramide?
Of denk je dat het toch een driehoek moet zijn? Zoek het maar uit!
En wist je dat de helft van een gelijkzijdige driehoek
de wonderen van de stelling van Pythagoras in zich heeft?
Hier zijn prachtige figuren mee te maken.
Ik raak er niet over uitgespeeld.
Natuurlijk is wiskunde heel belangrijk bij het bouwen van een huis.
Of een groot gebouw.
Of een kathedraal.
Daar hebben ze zich al in de meest grijze oudheid mee bezig gehouden.
De oude tempels van vele duizenden jaren geleden
geven al een duidelijk harmonieus wiskundig perspectief te zien.
Wat daarbij belangrijk is is de oppervlakte.
Hoe maak je van een vierkant een twee keer zo groot vierkant?
En wat is dan 'twee keer zo groot'?
Twee vierkanten op elkaar geeft een rechthoek, maar geen vierkant.
En drie vierkanten om de vierkant heen geeft wel een heel groot vierkant
maar is dat echt 'twee keer zo groot'?
De oppervlakte is in ieder geval vier keer zo groot.
Hoe maak je dan een oppervlakte die precies twee keer zo veel is als de oppervlakte van de basisvierkant, en het is toch een prachtig vierkant? Dat is dus niet zo eenvoudig. Daar kan je dus ook niet zoveel mee. Hoe dan te bouwen. Wel met de Gulden Snede. Maak het maar eens. Een punt T op een lijn AB blijkt daarbij belangrijk te zijn.
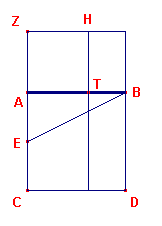
Hoe dat punt te berekenen?
Het is op het internet gezet, zie de weergave van
Dick Kingens
Als men in de wiskunde-site, die nu open gaat, klikt op dit figuurtje: 
en daarna links onder de tekening met cirkels het pijltje aanklikt, komt men bij een animatie van de constructie.
Neem passer en liniaal en potlood in de hand en maak het maar na!
Een leuke bezigheid, heb ik ontdekt.
Dit hele tweede boek van de elementen is trouwens de moeite waard voor wiskundige puzzelaars
die zich niet dagelijks met wiskundige stellingen bezig houden en het toch leuk vinden!
Dick Klingens heeft heel veel rond van alles wat met meten te maken heeft, op het web gezet!
|
die tot in het oneindige toe te herhalen is kan met dit magische punt T.
Teken bovenstaand figuur maar eens na,
2. Leg daarnaast TH*B en langs de andere zijde xTBD 3. Nu heb je een nieuw vierkant, namelijk met de grootte ABCD.
4.En zo kun je ook weer het grotere vierkant maken Je krijgt dan weer een groter vierkant.
en xTBD een kwartslag te draaien komt vierkant ABCD te voorschijn En AZ*B is even groot als CATx
|
dus ga dit nu maar eens gauw doen!
De Gulden snede is ook op een andere manier uit te leggen. Ik vond deze omschrijving:
|
Wanneer wij een voorwerp van een bepaalde lengte, b.v van 1 meter (een lat, een stok, een gespannen koord) op een willekeurige plaats doorsnijden, dan verdelen wij die lengte in twee stukken, die in de regel niet even lang zijn maar tussen wier lengte een zekere verhouding bestaat. Maar ook staan beide stukken in een zekere verhouding tot de gehele lengte. Alleen in één geval is die verhouding eenvoudig, namelijk als wij de bovengenoemde 100 cm precies in tweeën delen. Dan zijn de beide stukken elk 50 cm lang en zij verhouden zich tot de gehele lengte als 0,5:1, als 50:100. Verdelen wij nu die 100 cm in een kleinste stuk van 40 cm en een grootste stuk van 60 cm, dan verhoudt zich het kleinste stuk tot het grootste als 40:60 of als 0,667:1. Het grootste stuk verhoudt zich tot de gehele lengte als 60:100 of als 0,600:1. Wij merken hierbij op dat de waarde 0,667 groter is dan 0,600. Verdelen wij nu de 100 cm in een kleinste stuk van 35 cm en een grootste stuk van 65 cm, dan verhoudt zich het kleinste stuk tot het grootste als 35:65 of als 0,539:1. Het grootste stuk verhoudt zich tot de gehele lengte als 65:100 of als 0,650:1. In dit geval is de waarde 0,539 kleiner dan 0,650. Nu moet er dus ook een verdeling te vinden zijn, waarbij de verhouding tussen het kleinste en het grootste stuk even groot is als de verhouding tussen het grootste stuk en het geheel. Die verdeling kan met behulp van algebra worden vastgesteld en dan bedraagt de lengte van het kleinste stuk 38,2 cm en die van het grootste stuk 61,8 cm. Het kleinste stuk verhoudt zich dan tot het grootste als 38,2:61,8 of als 0,618:1, en het grootste stuk verhoudt zich tot de gehele lengte als 61,8:100 of als 0,618:1.
|
Er is nog meer over de gulden snede te vertellen.
Bijvoorbeeld, hoe maak je met de gulden snede een Pentagram!
kom deze week nog maar eens terug!
onder constructie
| ga terug naar de inhoud |
als je wilt communiceren over deze website kun je kontakt opnemen met Berthe Broeils
bijgewerkt op 2904 2003
