11.1.

Stelling van Phytagoras

11.1.1.

Algemeen

De stelling van Phytagoras is waarschijnlijk de meest bekende stelling in de wiskunde en één van de oudste stellingen uit de oudheid. Maar is deze stelling eigenlijk wel van Phytagoras?
Al ver voor Phytagoras hadden de Egyptenaren en vooral de Babyloniërs een verband gevonden tussen drie gehele getallen. Dit is hetzelfde verband dat ook in de stelling van Phytagoras is vastgelegd.

Door een Engelse archeoloog, genaamd Plimpton, is een babylonische schrijftablet gevonden, 1900-1600 voor het jaar nul. Op dit tablet heeft een schriftgeleerde vijftien combinaties van drie getallen aangegeven die er uiteindelijk allen op neerkomen dat de som van de kwadraten van twee van de drie getallen gelijk is aan het kwadraat van het derde getal. Dit was meer dan duizend jaar vóór de geboorte van Phytagoras.

Klik hier voor de geschiedenis van Phytagoras

11.1.2.

Uitleg

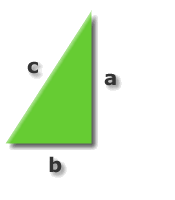
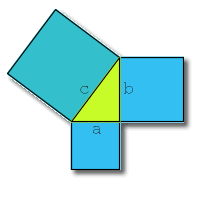
De stelling legt verband tussen de lengte van de hypotenusa (dit is de schuine zijde) van de rechthoekige driehoek en de lengten van de andere zijden, ook wel rechthoekszijden genoemd.

a en b zijn de rechthoekige zijden van de driehoek;
c is de hypotenusa.

De stelling van Phytagoras luidt als volgt;

"Voor elke rechthoekige driehoek geldt dat het kwadraat van de hypotenusa gelijk is aan de som van de kwadraten van de rechthoekige zijden".

In algebraïsche vorm:
a² +b² = c²

 

Grafisch weergegeven:

De som van de oppervlakten van de kleine vierkanten is gelijk aan de oppervlakte van het grote vierkant.

11.1.3.

Bewijzen voor de stelling

Er zijn vele bewijzen van de stelling bekend. Er is zelfs een boek in de omloop met 397 bewijzen.
Een paar bewijzen zal ik behandelen. Deze bewijzen zijn het meest bekend en gemakkelijk te onthouden

Bewijs 1

Deze constructie start niet met een rechthoekige driehoek, maar we beginnen met 2 vierkanten met een willekeurige afmeting..

  1. Plaats 2 vierkanten met respectievelijke zijden a en b naast elkaar. De totale oppervlakte is de 2 oppervlakten te samen, n.l.: a² + b²
  2. We tekenen nu 2 driehoeken, elk met een zijde a en zijde b en een hypotenusa (schuine zijde) c.
  3. Als laatste stap verplaatsen we de driehoeken 1 en 2 (90 graden om het middelpunt)

Het resultaat is een nieuw vierkant met zijden c en een oppervlakte c²

Dus het bewijs:

 a² +b² = c²
 

Bewijs 2

We starten met 4 gelijke driehoeken. 3 ervan zijn telkens 90° gedraaid.:

Elke driehoek heeft een oppervlakte van

Wanneer de 4 driehoeken tegen elkaar gelegd worden, ontstaat er een vierkant met de zijden (a + b), met daarin een vierkant gat met zijden c.
De oppervlakte van het grote vierkant met zijden (a + b) is gelijk aan de oppervlakte van het vierkant gat, met zijden c, plus de oppervlakten van de 4 driehoeken.

In formulevorm:

Werken we dit verder uit dan ontstaat:

Dus het bewijs:

 a² +b² = c²

Bewijs 3

We starten weer met 4 gelijke driehoeken zoals in bewijs 2.
Wanneer de 4 driehoeken tegen elkaar gelegd worden, zoals in het figuur is weergegeven, ontstaat er een vierkant met de zijden c, met daarin een vierkant gat met zijden (a - b).

De oppervlakte van het grote vierkant, met zijden c, is gelijk aan de oppervlakte van het vierkant gat plus de oppervlakten van de 4 driehoeken.

In formulevorm:

Werken we dit verder uit dan ontstaat:

Dus het bewijs:

 a² + b² = c²