De stelling van Pythagoras Volgens de stelling van Pythagoras heeft het vierkant, beschreven op de zijde tegenover de rechte hoek, een even groot oppervlak als de vierkanten beschreven op de twee andere zijden samen. Dit levert de bekende algebraïsche formule a2 + b2 = c2 op. Anders gezegd: het kwadraat van de schuine zijde van een rechthoekige driehoek is gelijk aan de som van de kwadraten van de beide rechthoekszijden. Als je aan een tangram de naam van een beroemde wiskundige meegeeft, dan wil je toch wel even controleren of de tangram kan voldoen aan deze stelling, of niet soms? Vandaar dit uitstapje en na wat puzzelen, knippen en plakken is het bewijs snel geleverd! 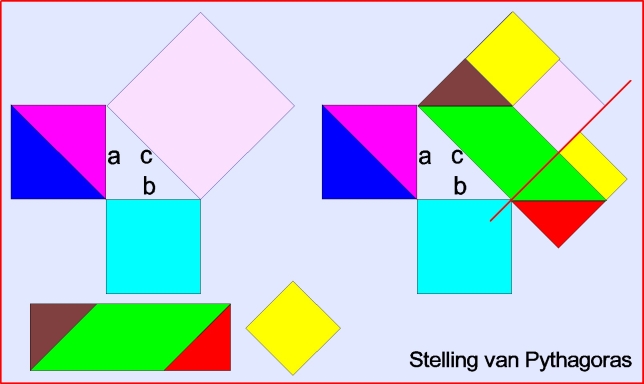Voor het bewijzen van de stelling worden de tangramstukjes bijvoorbeeld als volgt gerangschikt: 1. De paarse en blauwe driehoeken worden samengevoegd tot een vierkant (zijde a). 2. Het lichtblauwe vierkant is net zo groot als het paars/blauwe vierkant (zijde b). 3. De tegenoverliggende zijde c van de hieruit ontstane driehoek dient als basis voor een vierkant vlak, hier lichtrose ingekleurd, waarin dan de rest van de tangramstukjes moet passen om aan de stelling van Pythagoras te kunnen voldoen. Dat kan eenvoudig grafisch worden weergegeven. De bruine en rode driehoeken zijn toegevoegd aan de uiteinden van de groene ruit en hierdoor ontstaat een lange, smallere rechthoek. Samen met het overblijvende gele vierkant wordt het rose vlak opgevuld, maar de lange rechthoek steekt dan over! Gemakkelijk is te zien, dat het overstekende gedeelte onder de rode lijn net zo groot is als het gele vierkant (dat boven tweemaal in dat rose vlak past) en voor het totale inzicht is dit gele vierkant nog eens onder het overstekende gedeelte gelegd: het past precies! Hiermee is bewezen dat deze tangram helemaal voldoet aan de stelling van Pythagoras en dus met recht zo mag worden genoemd!