Burgers' Creep
a program for the Texas Instruments TI-83
and TI-84 (Plus) graphing calculators

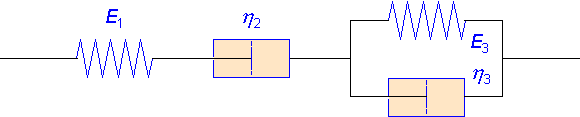
Summary

The Burgers model is a simple mathematical model which illustrates the nature of real mechanical behaviour of amorphous polymers and other materials with both elastic and viscous nature. The model consists of a Maxwell element joined in series with a Voigt (or Kelvin) element. Maxwell's element can be visualized as a Hookean spring and a Newtonian dashpot in series, thus having viscoelastic properties by combining one elastic parameter (E₁) and one viscous parameter (η₂). Similarly, the Voigt element obtains viscoelasticity as a result of placing a Hookean spring and a Newtonian dashpot in parallel.

Using the Burgers model the program simulates creep. At time t = 0 a fixed tension (tensile stress) is applied to a polymer sample which can be represented by a Burgers model with known parameters. Each of the three elements in series will elongate in a different way.
• The Maxwell spring undergoes an instant elastic deformation. It elongates instantly and completely.
• The deformation of Maxwell's dashpot is directly proportional to time. The creep is irreversible.
• Thirdly, the Voigt element undergoes a delayed elastic deformation and the creep is reversible.
• Adding the three elongations yields the time-dependent elongation of the Burgers model as a whole.
The program draws a line for each of these four elongations as a function of time.

The stress and parameter input values used in the program listing below are adopted from problem 3 of the preliminary examination example Polymeren II. For a better understanding of the calculations that are being executed, consult the solution help at page 4 of this document. You can download Polymeren II from here.

After running the program with the given example input values, the graph is displayed in a window with time values along the horizontal x-axis ranging from 0 to 800 s. The elongation (or strain) values along the y-axis range from ε = 0 to ε = 0,07 (7 %).

To retrieve elongation and time values from the four displayed lines, use the TRACE key and the CALC function (2nd, CALC keys). Time is expressed in seconds.

Using the TABLE function is another option. Just press the 2nd, TABLE keys. The right arrow key enables viewing the elongations of the Voigt element in the fourth column of the table and the elongations of the Burgers model as a whole in the fifth column. You may wish to call upon the TBLSET function to adjust the table settings.

Press CLEAR to return to the normal screen.
Press GRAPH to show the graph again.
At the normal screen, press 2nd, ENTRY, ENTER to restart the program CREEP.

After running the program with other input values, the presented graph may need some changes for the better. For instance, if the total strain at 800 s exceeds 7 %, use the WINDOW key to adjust Ymax in the WINDOW-menu, then press the GRAPH key to draw the new diagram. Now, if the default Yscl value of 1 % isn't satisfying any more, press the WINDOW key again, and so on.