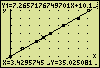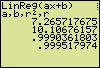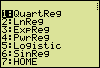SummaryEvery measurement is influenced by many uncertainties. Measurement uncertainties can never be completely eliminated, so the true value for any quantity is never known exactly.
Linear regression is a statistical tool that helps you to determine the "best-fitting" straight line for any given set of experimental data. In the relationship y = ax + b the constants a and b are being determined. The obtained function hands over which value is to be expected on an average for the one variable (y) at a given value of the other variable (x).
Quadratic regression produces the "best" parabola for a set of experimental data by calculating the constants a, b, and c of the quadratic equation y = ax² + bx + c. Other regression models available in the program: |
Program Listing |
Help |
| PROGRAM:REGRESS | R : ALPHA, R keys |
| ClrHome | > PRGM > I/O > ClrHome |
| RectGC:CoordOn | > 2nd, FORMAT > ... : : ALPHA, : keys |
| GridOn:AxesOn | |
| LabelOn:ExprOn | |
| PlotsOff | > 2nd, STAT PLOT > PlotsOff |
| FnOff | > VARS > Y-VARS > On/Off... > ... |
| GraphStyle(1,1) | > PRGM > CTL > GraphStyle , : comma key |
| 1 → Xres | "→" Symbolizes the STO> key > VARS > Window... > Xres |
| Disp "VALUES IN L1,L2" | > PRGM > I/O > Disp Space: ALPHA, .. (above 0 key) L1 : 2nd, L1 |
| 0 → Z : While Z<40 | > PRGM > CTL > While > 2nd, TEST > "<" |
| Z+1 → Z:End | > PRGM > CTL > End |
| (max(L1)–min(L1))/5 → U | > MATH > NUM > max( |
| 10^(int(log(U))) → Z | 10^( : 2nd, 10x keys > MATH > NUM > int( |
| U/Z → U | |
| (int(√(U–1))²+1)Z → Xscl | √( : 2nd, √ keys (square root) ² : x² key > VARS > Window... > Xscl |
| (max(L2)–min(L2))/5 → V | |
| 10^(int(log(V))) → Z | |
| V/Z → V | |
| (int(√(V–1))²+1)Z → Yscl | √( : square root Xscl and Yscl will be set to 1, 2, or 5 times a power of ten. |
| Plot1(Scatter,L1,L2, §) | > 2nd, STAT PLOT > Plot1( > 2nd, STAT PLOT > TYPE > Scatter > 2nd, STAT PLOT > MARK > § (small square) |
| ZoomStat | > ZOOM > ZoomStat |
| ZoomSto | > ZOOM > MEMORY > ... |
| Lbl 0 : ClrHome | > PRGM > CTL > Lbl > PRGM > I/O > ClrHome |
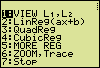
| Menu("","VIEW L1,L2",1, "LinReg(ax+b) ", 2, "QuadReg ",3, "CubicReg ",4, "MORE REG",50, "ZOOM,Trace", 60, "Stop",7) | > PRGM > CTL > Menu( > STAT > CALC > LinReg(ax+b) > TRACE > PRGM > CTL > Stop |
| Lbl 50 | |
| Menu("","QuartReg ", 51, "LnReg ",52, "ExpReg ",53, "PwrReg ",54, "Logistic ",55, "SinReg ",56, "HOME",57) | > STAT > CALC > CubicReg etc. |
| Lbl 60 | |
| Menu("","Zoom Out",61, "Zoom In",62, "RESET ZOOM",63, "Trace",64, "HOME",65) | |
| Lbl 1 | |
| Output(1,1,L1) | > PRGM > I/O > ... |
| Pause :ClrHome | > PRGM > CTL > Pause |
| Output(1,1,L2) | |
| Pause | |
| Goto 0 | > PRGM > CTL > ... |
| Lbl 2 | |
| Disp "LinReg(ax+b) ", "a,b,r²,r" | > STAT > CALC > LinReg(ax+b) > VARS > Statistics... > EQ > a (and b,r²,r) |
| LinReg(ax+b) Y1 | > VARS > Y-VARS > Function... > Y1 |
| Disp a,b,r²,r | > VARS > ... |
| Lbl 21 | |
| Pause | |
| DispGraph | > PRGM > I/O > DispGraph |
| Pause | |
| Goto 0 | |
| Lbl 3 | |
| Disp "QuadReg ", "Y=aX²+bX+c", "a,b,c,R²" | X : X key or ALPHA, X keys > VARS > Statistics... > EQ > R² |
| QuadReg Y1 | It needs 3 points at least (Reg-equation 4 at least). |
| Disp a,b,c,R² | > VARS > ... |
| Goto 21 | |
| Lbl 4 | |
| Disp "CubicReg Y=aX³+..", "a,b,c,d,R²" | Y=aX³+bX²+cX+d |
| CubicReg Y1 | It needs 4 points at least (Reg-equation 5 at least). |
| Disp a,b,c,d,R² | |
| Goto 21 | |
| Lbl 51 | |
| Disp "QuartReg a..e,R²" | Y=aX4+bX³+cX²+dX+e |
| QuartReg Y1 | It needs 5 points at least (Reg-equation 6 at least). |
| Disp a,b,c,d,e,R² | |
| Goto 21 | |
| Lbl 52 | |
| Disp "LnReg ", "Y=a+bln(X)", "a,b,r²,r" | |
| LnReg Y1 | |
| Disp a,b,r²,r | |
| Goto 21 | |
| Lbl 53 | |
| Disp "ExpReg ", "Y=a*b^X", "a,b,r²,r" | |
| ExpReg Y1 | |
| Disp a,b,r²,r | |
| Goto 21 | |
| Lbl 54 | |
| Disp "PwrReg ", "Y=a*X^b", "a,b,r²,r" | |
| PwrReg Y1 | |
| Disp a,b,r²,r | |
| Goto 21 | |
| Lbl 55 | |
| Disp "Logistic ", "Y=c/(1+ae^(–bX))", "a,b,c" | |
| Logistic Y1 | |
| Disp a,b,c | |
| Goto 21 | |
| Lbl 56 | |
| Disp "ESTIMATE PERIOD" | |
| Input T | |
| ClrHome | |
| Disp "SinReg ", "Y=a*sin(bX+ c)+d", "a,b,c,d" | |
| SinReg 16,L1,L2,T,Y1 | It needs 4 points at least; 2 points per period. |
| Disp a,b,c,d | The results bX and c are always expressed in radians. |
| 2π/abs(b) → T | π : 2nd, π keys (pi) |
| Pause | |
| Disp "PERIOD, FREQ.",T,1/T | Once the period is calculated, its value may be used to iterate once more, especially when b is a negative. |
| Goto 21 | |
| Lbl 57:Goto 0 | |
| Lbl 61 | |
| √(2) → Z : Z → XFact | (square root) |
| Z → YFact | > VARS > Window... > X/Y > Xfact |
| 10^(int(log((Xmax–Xmin)/Z))) → Xscl | |
| 10^(int(log((Ymax–Ymin)/Z))) → Yscl | |
| Zoom Out | > ZOOM > Zoom Out |
| Pause | |
| Goto 60 | |
| Lbl 62 | |
| Zoom In:Pause | |
| Goto 60 | |
| Lbl 63 | |
| ZoomRcl:Pause | > ZOOM > MEMORY > ZoomRcl |
| Goto 60 | |
| Lbl 64:Trace | > TRACE |
| Goto 60 | |
| Lbl 65:Goto 0 | |
| Lbl 7 | |
| Xscl → ΔTbl:Stop | > VARS > Table... > ΔTbl (Delta-Tbl) > PRGM > CTL > Stop |
An ApplicationAfter putting in the program listing, you might like to see the program working. Try this example.
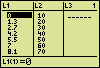
The ExperimentA long tube is placed vertically and filled with a viscous liquid. (Which liquid is not?) When a bullet, being made up of steel, is let loose in the liquid, the sinking speed soon becomes constant. To determine this constant velocity, the position x is measured as a function of time t. The measuring outcome is:
Entering the ValuesThe time t is considered the independent variable and is measured along the horizontal axis of a graph. The position x, the dependent variable, is measured along the vertical axis. List 1 (L1) must contain values of the variable, which is to be plotted along the horizontal axis.
Getting the Linear Equation and the Coefficient of CorrelationAfter preparing L1 and L2, run the program. A menu appears.
The produced value of the coefficient of correlation (r = 0,99952) indicates that the found linear equation is only a fair representation of the relationship between the measured t and x values. Counting the nines, that directly follow the comma in the coefficient of correlation, is a convenient way to find out the usefulness of the equation. In chemical and physical determinations the number of nines may be interpreted in this way: five nines mean an excellent representation, four nines a good one, three nines a fair one, two nines a poor one, and one nine means a very poor representation. With no nines directly behind the comma the equation is "unusable".
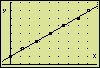
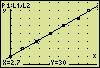
Viewing the Plotted Points and the Straight LinePress ENTER.
TracingOnce the graph has been drawn, press ENTER, select option "6:ZOOM,Trace" in the menu, and "4:Trace" in the following sub-menu. Next, use the left and right arrow keys to trace the values of the plotted measuring points.
Press the up arrow key once to enable tracing the plotted line. Again, use the left and right arrow keys to explore the coordinates of some points of the line.
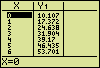
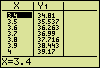
Using the TABLE function is another way to get these values. Stop the execution of the program by selecting "5:HOME" in the sub-menu and "7:Stop" in the main menu. Then call on the TABLE function. You may have to adjust the table settings using the TBLSET function.
Other ApplicationsIn other applications more regression methods may be needed. Selecting "5:MORE REG" in the main menu allows access to other regression functions in the following sub-menu.
|
Hein ten Horn
Top | Programs Texas Instruments | Home