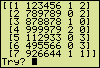A Mastermind game based on numerals instead of colorsPlay the familiar game Mastermind with numerals instead of colors and have a hunt for a secret number. The random number is generated by your calculator. Available 'colors' are the numerals from 1 to 9.
The second examination 5678 leads to [1 1], meaning one right numeral at the right position and one right numeral at a wrong position. From both responses it follows that the number in demand holds no nines.
(TI images. The screen examples
In case of a six digit number the game could pass as follows.
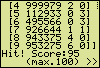
The first two outcomes indicate a double or triple presence of a numeral in the unknown number. After seven examinations only four possible numbers remain:
Memory overflow |
Program Listing[ Remarks ]MASTRMND Rem MEM IJKZ mat ABC Rem VER200410 [ > 2ndF,PRGM > PRGM > Rem ] [ > MATRIX > NAME > mat A ] ClrT [ > 2ndF,PRGM > SCRN > ClrT ] Print "** MASTERMIND ** Print " Print "BE SURE FSE IS Print "SET TO FLOATPT Print " Print "(SEE SET UP) Print " Print ">> [ > MATH > INEQ > ">" ] Wait 4→K [ → : STO-key ] Label A0 [ > 2ndF,PRGM > BRNCH > Label ] [ A0, not AO ] int K→K [ > MATH > NUM > int ] min(max(3,K),8)→K int (1+9rnd_mat(4,K))→mat A [ > MATRIX > OPE > rnd_mat( ] K+2→Z (ln(396/391)/ln 2)^.5→J [ ^ : ab-key ] (1–1.5J)/(1–J)*Z→mat A(4,1) (1.5Z–mat A(4,1))^2/ln 2→mat A(4,2) {1,4}→dim(mat B) fill(0,mat B) Label A1 ClrT Print "** MASTERMIND ** Print " Print "FIND A NUMBER OF Print K Print "DIGITS. Print "ENTER DIGITS. (HELP:0) Label A2 0→Z Input Z abs(Z)→Z If Z<.1*10^K Goto C0 [ mark the decimal point ] (Z–fPart Z)/10^K→Z Z–int Z→Z Z*10^K→mat B(1,2) 0→mat B(1,3) 0→mat B(1,4) Z→mat A(4,3) row_mult(0,mat A,1)→mat A [ > MATRIX > OPE > row_mult( ] row_plus(mat A,3,1)→mat A 0→J Label A3 J+1→J 10mat A(4,3)→mat A(4,3) int mat A(4,3)→mat A(2,J) If mat A(2,J)=0 Goto C0 mat A(4,3)–mat A(2,J)→mat A(4,3) If J<K Goto A3 0→J Label B0 J+1→J J→I If mat A(1,J)≠mat A(2,I)Goto B1 mat B(1,3)+1→mat B(1,3) -1→mat A(1,J) [ negation symbol (-), [ not subtraction symbol ] -2→mat A(2,I) Label B1 If J<KGoto B0 0→J Label B2 J+1→J 0→I If mat A(1,J)=-1Goto B5 Label B3 I+1→I If mat A(1,J)≠mat A(2,I)Goto B4 mat B(1,4)+1→mat B(1,4) -1→mat A(1,J) -2→mat A(2,I) K→I Label B4 If I<K Goto B3 Label B5 If J<K Goto B2 mat B(1,1)+1→mat B(1,1) If mat B(1,1)=1 Goto B6 trans augment(trans mat C,trans mat B)→mat C [ > MATRIX > MATH > trans ] Goto B7 Label B6 mat B→mat C Label B7 ClrT Print mat C If mat B(1,3)<K Goto A2 Print "HIT! SCORE (MAX.100): mat A(4,1)–mat B(1,1)→Z e^(Z*abs(Z)/mat A(4,2))→Z [ e^ : 2nd,ex ] min(Z,1)→Z (mat B(1,3)+.7mat B(1,4))/K→J 10+90*(.56J+.44Z)*J→Z int((Z+.5)/5)*5→Z Print Z Wait Goto A0 Label C0 ClrT Print "VALID DIGITS: 1-9 Print " Print "INVALID ATTEMPTS Print "(EXAMPLES): Print "3303, 0003, 3 Print " Print ">> Wait :ClrT Print "RESPONSE: Print "1 ATTEMPT NUMBER Print "2 YOUR TRY Print " NUMBER OF RIGHT [ 2 spaces in front of "NUMBER" ] Print " DIGITS AT [ 2 spaces in front of "DIGITS" ] Print "3 RIGHT POSITION Print "4 WRONG POSITION Print ">> Wait :ClrT Print "CHANGE NUMBER OF Print "POSITIONS: 3-8 Print "STOP:0 RESUME: [ 7 spaces in front of "RESUME:" ] Print K Print "INFO: WWW.TENHORN.COM Print " K→Z:Input Z ClrT If Z=0 Goto C1 If (Z=K) and (mat B(1,1)>0) Goto C2 [ > MATH > LOGIC > and ] Z→K Goto A0 Label C1 {1,1}→dim(mat C) mat C→mat A mat C→mat B Print "PRESS CL End Label C2 Print mat C Goto A2
If you need help with programming your calculator, this exercise will put you on the way: Creating a Program for the Sharp EL calculator |
Hein ten Horn
Top | Programs Sharp EL | Home

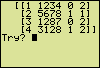
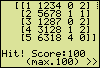
 This Mastermind game can be played at different levels of difficulty. Just make the program generate a random number with more or less digits. To do so, put in a "0", press Enter more than once to pass through some help screens and select 3, 4, 5, 6, 7 or 8 digits.
This Mastermind game can be played at different levels of difficulty. Just make the program generate a random number with more or less digits. To do so, put in a "0", press Enter more than once to pass through some help screens and select 3, 4, 5, 6, 7 or 8 digits.