Opgaven natuurkunde
|
Opgaven in alfabetische volgorde Driftsnelheid (elektriciteit) Fontein (vloeistoffen, dynamica) Fototoestel (geometrische optica) Glasplaat (geometrische optica) Heupgewricht (statica) Liftcabine (dynamica) Luchtballon / Parachutist (numerieke natuurkunde, dynamica) Motorrijder (dynamica) Noodlanding (arbeid, energie) Sprint (kinematica) Verkeerslichtenregeling (digitale signaalverwerking, logische schakelingen) Warmtewisselaar (warmte) Waterput (kinematica, numerieke natuurkunde) Weerstandsnetwerkje (elektriciteit) Zonnepaneel (elektromagnetische straling, warmte) |
• Driftsnelheid - (elektriciteit)
In de veronderstelling dat er gemiddeld één geleidingselektron per metaalatoom beschikbaar is, bevat koper 8,5·1028 geleidingselektronen (vrije elektronen) per m3.
Of, in een andere formulering, de (vrije) elektronenconcentratie is 8,5·1028 m−3.
a. Bereken de elektronenconcentratie in drie significante cijfers.
Over elektrische stroom wordt wel eens beweerd dat de elektrische lading met grote snelheid door het snoer van een huishoudelijk apparaat gaat.
b. Ga voor gelijkstroom na of die bewering waar is. Bereken daartoe de gemiddelde snelheid waarmee geleidingselektronen naar de 'pluspool' verplaatst worden in een koperdraad die een cirkelvormige doorsnede met een diameter van 1,0 mm heeft en waarin de stroomsterkte 0,26 A bedraagt.
(Ter vergelijking: de effectieve stroomsterkte in een gloeilamp van 60 watt die brandt op de wisselspanning van 230 volt van het lichtnet, is ook 0,26 ampère.)
• Fontein - (vloeistoffen, dynamica)
 In de aanvoerleiding van een fontein moet de druk in het water voldoende groot zijn om de waterstraal tot een hoogte van 12 meter boven de spuitmond te laten reiken.
In de aanvoerleiding van een fontein moet de druk in het water voldoende groot zijn om de waterstraal tot een hoogte van 12 meter boven de spuitmond te laten reiken.
Er wordt een spuitrichting aangehouden die een weinig afwijkt van precies verticaal omhoog. Hiermee wil men voorkomen dat de waterstraal door terugvallend water wordt gehinderd in het bereiken van de gewenste hoogte.
Bijgaande figuur is niet op schaal.
De aanvoerleiding heeft een inwendige diameter van 6,2 cm. Via een spuitmond met kleinere inwendige diameter (1,8 cm) komt het water in de buitenlucht waar een druk van 1010 hPa heerst. De opening van de spuitmond (B) bevindt zich 2,5 m boven de hartlijn van het horizontale gedeelte van de aanvoerbuis. De temperatuur van het water is 20 °C.
a. Vlak boven de spuitmond heeft de gebonden waterstraal een kleinere diameter dan hogerop. Verklaar dit.
b. Een pomp voorziet de fontein van water. Hoe groot is het te leveren volumedebiet?
c. Bereken de minimale druk van het water in de aanvoerleiding bij A die nodig is om het water tot de hoogte van 12 meter boven de spuitmond op te voeren.
d. In werkelijkheid zal de benodigde waterdruk bij A hoger uitvallen. Oorzaken zijn onder andere optredende drukverliezen in de leidingen door stromingsweerstand (samenhangend met de viscositeit van de vloeistof en de turbulentie in het buizenstelsel, vooral in bochten en vernauwingen).
Geef nog drie andere mogelijke oorzaken.
e. Maak een schatting van het nuttige vermogen van de pomp.
• Fototoestel - (geometrische optica)
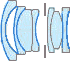 In een digitale camera wordt het fotografische beeld door een objectief ontworpen op de sensor van een chip. Een objectief is een samengestelde lens. De tekening toont een voorbeeld in doorsnede. Hierin zijn twee positieve lenzen en vijf negatieve lenzen te onderscheiden. Fototoestellen zijn uitgerust met een objectief omdat zo'n stelsel lenzen beelden van hogere kwaliteit kan produceren dan een enkele lens. Bij het beantwoorden van de vragen in deze opgave mag je het objectief opvatten als een gewone enkelvoudige positieve lens.
In een digitale camera wordt het fotografische beeld door een objectief ontworpen op de sensor van een chip. Een objectief is een samengestelde lens. De tekening toont een voorbeeld in doorsnede. Hierin zijn twee positieve lenzen en vijf negatieve lenzen te onderscheiden. Fototoestellen zijn uitgerust met een objectief omdat zo'n stelsel lenzen beelden van hogere kwaliteit kan produceren dan een enkele lens. Bij het beantwoorden van de vragen in deze opgave mag je het objectief opvatten als een gewone enkelvoudige positieve lens.
 De chip met de sensor is van het type CCD (charge-coupled device) of van het in nieuwe camera's meer en meer aangetroffen type CMOS (complementary metal oxide semiconductor). Een voorbeeld van een CMOS-chip zie je hiernaast. De sensor is het rechthoekige vlak binnen het blauwe kader. Daar bevinden zich lichtgevoelige elementen (pixels) die het beeld op de sensor helpen omzetten in elektronische (digitale) informatie. De pixels zijn op gelijke pixelafstanden (hart-hart) in rijen en kolommen gerangschikt.
De chip met de sensor is van het type CCD (charge-coupled device) of van het in nieuwe camera's meer en meer aangetroffen type CMOS (complementary metal oxide semiconductor). Een voorbeeld van een CMOS-chip zie je hiernaast. De sensor is het rechthoekige vlak binnen het blauwe kader. Daar bevinden zich lichtgevoelige elementen (pixels) die het beeld op de sensor helpen omzetten in elektronische (digitale) informatie. De pixels zijn op gelijke pixelafstanden (hart-hart) in rijen en kolommen gerangschikt.
Op een afstand van 19 meter voor het objectief van een CMOS-fototoestel staat een 15 meter brede gevel van een gebouw. De beeldsensor is 36 mm breed en 24 mm hoog en bestaat uit 21,026 miljoen pixels.
Met een telelens die een brandpuntsafstand van 135 mm heeft, verschijnt maar een gedeelte van het gebouw in het beeld op de sensor. Door uit te zoomen of door een objectief met een kleinere brandpuntsafstand te gebruiken moet het wél mogelijk zijn het hele gebouw op de foto te krijgen.
a. Bereken de grootste brandpuntsafstand waarmee de volle breedte van de gevel op de breedte van de beeldsensor kan worden afgebeeld.
 De foto wordt gemaakt met een brandpuntsafstand van 35 mm.
De foto wordt gemaakt met een brandpuntsafstand van 35 mm.
Op een gevelsteen van het gebouw staat een jaartal waarin het Romeinse cijfer "I" voorkomt. De drie lijnen in dit symbool zijn maar 7 mm dik, waarmee de vraag rijst of het jaartal nog leesbaar is op een afdruk van de (onbewerkte) digitale foto. Daartoe mag de breedte van de lijntjes in het sensorbeeld niet (veel) kleiner zijn dan de pixelafstand.
b. Hoeveel pixels breed is zo'n lijntje in het beeld op de sensor?
Een toeristisch informatiebord staat 7,0 m voor de lens. De tekst op het bord verschijnt niet scherp op de foto. Dit ligt voor de hand want de camera is scherp ingesteld op 19 m. Toch wordt ook de weergave van voorwerpen in een beperkte ruimte vóór en een grotere ruimte achter het vlak van scherpstelling als scherp waargenomen wanneer het sensorbeeld op gangbare afstanden bekeken wordt op het beeldscherm van een computer, op een fotoafdruk of op het projectiescherm van een beamer. De diepte van beide ruimten samen, de zogenoemde scherptediepte, hangt onder meer af van het op het fototoestel ingestelde diafragmagetal. Zie het diagram.

Bij elk diafragmagetal horen twee curven. Ze geven de voorste en achterste grens van de scherptediepte als functie van de ingestelde voorwerpsafstand. De rode pijlen laten een concreet voorbeeld zien: met de instellingen voorwerpsafstand = 8,0 m en diafragmagetal = 2,0 wordt de weergave van alle voorwerpen op afstanden tussen 5,8 m en 13,1 m scherp genoemd (bij de gegeven brandpuntsafstand f en scherpte-eis c). Alleen het beeld van een voorwerpspunt op 8,0 m (op de blauwe lijn) is haarscherp, maar de weergave van de punten dichterbij en verderaf wordt ook als scherp ervaren omdat het natuurkundige beeld van die punten op een voldoend kleine afstand achter of vóór het sensorvlak ligt.
Uit de grafiek blijkt verder nog dat een groter diafragmagetal gekozen moet worden om een grotere scherptediepte in het motief te krijgen. De effectieve lensopening neemt hierbij af. De volgende afbeelding van een '50-mm-objectief' illustreert dit voor de diafragmagetallen 1,4, 2,8 en 16. Het diafragma van het objectief bevat echter zeven lamellen waarmee een traploze instelling van het diafragmagetal (de diafragmawaarde) mogelijk is.

f/d = 1,4 f/d = 2,8 f/d = 16 (f = 50 mm)
Het kiezen van een ander diafragmagetal beïnvloedt ook het lichtvermogen dat door de lens gaat want:
(1) diafragmagetal = f/d = brandpuntsafstand / (diameter van de diafragmaopening);
(2) de oppervlakte van de opening is recht evenredig met het kwadraat van de diameter;
(3) de lichtstroom is recht evenredig met de oppervlakte van de diafragmaopening.
In de reeks diafragmagetallen ...- 4 - 2,8 - 2 - 1,4 -... nemen de waarden af met een factor √2. Elke stap in afnemende richting betekent dus een verdubbeling van de lichtstroom in de lens!
c. Verklaar dit nader. Je mag hierbij een cirkelvormige diafragmaopening met oppervlakte π·r2 veronderstellen.
 De onscherpe weergave van de tekst van het eerder genoemde informatiebord op de voorgrond van het gezichtsveld ontstaat bij het diafragmagetal 2,0 en de sluitertijd (1/500) s of 2,00 ms; daarnaast zijn er ook nog de brandpuntsafstand 35 mm en de voorwerpsafstand 19 m (het fototoestel is scherp ingesteld op de gevel van het gebouw). De belichting is bij deze instellingen correct. De foto is dus niet over- of onderbelicht.
De onscherpe weergave van de tekst van het eerder genoemde informatiebord op de voorgrond van het gezichtsveld ontstaat bij het diafragmagetal 2,0 en de sluitertijd (1/500) s of 2,00 ms; daarnaast zijn er ook nog de brandpuntsafstand 35 mm en de voorwerpsafstand 19 m (het fototoestel is scherp ingesteld op de gevel van het gebouw). De belichting is bij deze instellingen correct. De foto is dus niet over- of onderbelicht.
d. Vooropgesteld dat andere aanpassingen ongewenst zijn, bij welke combinatie van diafragmagetal en sluitertijd is dan de weergave van zowel het informatiebord als het gebouw scherp, de belichting van de foto in orde en de kans op bewegingsonscherpte zo klein mogelijk?
e. Beide objecten zijn ook gelijktijdig scherp te krijgen door slechts één grootheid te wijzigen (in plaats van twee of meer). Welke grootheid is dat en wat is de nieuwe in te stellen waarde?
 Kleine scherptedieptes komen voor bij het fotograferen op korte afstand. In wat een dichtbij-opname heet is de voorwerpsafstand kleiner dan ongeveer tien keer de brandpuntsafstand. Volgens een iets ruimer criterium is de lineaire vergroting N tenminste 0,10.
Kleine scherptedieptes komen voor bij het fotograferen op korte afstand. In wat een dichtbij-opname heet is de voorwerpsafstand kleiner dan ongeveer tien keer de brandpuntsafstand. Volgens een iets ruimer criterium is de lineaire vergroting N tenminste 0,10.
Nader je echter de afstand waarop het voorwerp op ware grootte op de sensor of film wordt afgebeeld (N = 1), dan is macro-opname de specifieke term. In de macrofotografie is de lineaire vergroting ongeveer 0,3 of groter, maar meestal niet groter dan 5.
De duimstok op de foto rechts is in werkelijkheid 12 mm breed zodat de netto-vergroting op de meeste beeldschermen bij normale weergave zal neerkomen op een waarde tussen 1,5 en 3,0; dat maakt de opname echter nog geen macro-opname.
In de tekening hieronder is de vergroting van het beeld op de sensor 0,6. De afstand tussen de lens en de sensor is zó ingesteld dat het punt P haarscherp op het sensorvlak wordt afgebeeld. Dichterbij en verderaf gelegen punten zoals Q en R geven geen fijn puntje te zien maar een vervaagd lichtvlekje. Dit onscherpteschijfje op de sensor is onwerkelijk groot en met een groene kleur ingetekend. Voor sensoren ter grootte van 24 mm × 36 mm is de algemeen aanvaarde waarde voor de maximale toelaatbare diameter c van de onscherpteschijf (0,030 ± 0,003) mm. Gewoonlijk wordt 0,030 mm aangehouden.
Alle voorwerpspunten waarvan de diameter van de onscherpteschijf op de sensor niet groter is dan 0,030 mm beschouwt men als scherp afgebeeld. Voorwerpspunten die aan deze voorwaarde voldoen bevinden zich binnen de scherptediepte s.

(sensorgrootte en onscherpteschijf niet op schaal)
Door constructie van de vier lichtstralen die zowel langs een rand van de diafragmaopening als langs een rand van het kritische onscherpteschijfje lopen worden twee snijpunten gevonden die de beeldpunten moeten zijn van de punten Q en R op de randen van de scherptediepte.
De maximale toelaatbare diameter c is samen met de brandpuntsafstand f, de voorwerpsafstand v en het diafragmagetal f/d bepalend voor de positie van de twee grensvlakken van de scherptediepte s. Dit is af te leiden uit de tekening door voor de grootheden c, f, v en d afzonderlijk na te gaan welke invloed een verandering heeft op de loop van de vier lichtstralen.
f. Bepaal welke brandpuntsafstand in de tekening van toepassing is als de voorwerpsafstand 14,4 cm bedraagt. Bepaal daartoe eerst de lineaire vergroting N in drie significante cijfers.
g. Bepaal het gebruikte diafragmagetal.
h. Leg met behulp van het verloop van lichtstralen uit dat de scherptediepte toeneemt wanneer een groter diafragmagetal wordt ingesteld.
i. Een bekend probleem in de macrofotografie is de beperkte scherptediepte. In het voorbeeld hier (v = 14,4 cm, f en f/d zoals gevonden in de vragen f en g) bedraagt de scherptediepte maar 0,25 mm. Zelfs na diafragmeren tot het diafragmagetal 11 is de scherptediepte nog net geen 3,0 mm. De tekening toont echter een scherptediepte s die groter is dan de voorwerpsafstand van 14,4 cm. Hoe komt dat?
Stof en ander vuil op de lens of op de beeldsensor benadelen de kwaliteit van de foto.
j. Hoe wordt het beeld aangetast door aanwezigheid van stofjes op de sensor?
k. Wat is de aard van het kwaliteitsverlies bij stof op de lens? Licht het antwoord toe.
De maximale gezichtsscherpte (in de zin van scheidend vermogen) van het menselijk oog is een kleine boogminuut. Veelal werkt men met 1,0 boogminuut (1,0'). Dat wil zeggen dat het oog twee lijnen nog moeiteloos kan onderscheiden als ze gescheiden zijn door een gezichtshoek van (1/60)°. De lijntekening hieronder moet daartoe bekeken worden op een afstand van 34,4 keer de breedte van de figuur. Op de dubbele afstand, bij de gezichtshoek 0,5', worden nog slechts twee vervaagde, grijze vlakken waargenomen.
![]()
Anders dan bij het ongewapend oog is het scheidend vermogen van het fototoestel te beïnvloeden door de brandpuntsafstand te veranderen. Zo zal een telelens of ingezoomd objectief een smaller gezichtsveld (met kleinere tophoek) op de volle breedte van de sensor afbeelden dan een standaardobjectief (brandpuntsafstand 50 mm).
l. Bij welke brandpuntsafstanden kan de gegeven digitale camera qua scheidend vermogen beter presteren dan het menselijk oog?


De iris in het oog werkt als diafragma
(irisdiafragma merel).
• Glasplaat - (geometrische optica)
 De figuur hiernaast toont een glasplaat in zijaanzicht
De figuur hiernaast toont een glasplaat in zijaanzicht
(AB is de dikte van de plaat). De scherpe hoek bij punt C is 60°. De ≈-symbolen moeten aangeven dat BC en DA meer dan honderd keer zo lang zijn als AB.
Een lichtstraal treft het glasoppervlak CD in punt P en maakt een hoek α van 50° met het lijnstuk PD.
De voortplantingssnelheid van de gebroken lichtstraal in het glas is twee derde van de lichtsnelheid in lucht (of vacuüm). De lichtstraal verlaat de glazen plaat via een punt Q in het vlak BC (dit punt is niet ingetekend).
a. Hoe groot is de brekingsindex van het glas?
b. Bereken de hoek (β) tussen de bij Q uittredende lichtstraal en het lijnstuk QB.
We kunnen hoek α laten variëren tussen 0° en 180°. Bij bepaalde waarden van α treedt aan het vlak BC totale terugkaatsing op; bij andere waarden vindt hier wél breking plaats of valt de lichtstraal niet op het vlak BC.
c. Voor welke gehele waarden (afgerond) van hoek α treedt er aan het grensvlak BC zeker totale terugkaatsing op? Laat multireflectie buiten beschouwing.
• Heupgewricht - (statica)
Een opgetild been bevindt zich gestrekt in horizontale stand. In de tekening houdt 'n viertal uitwendige krachten het been in evenwicht: de spankrachten Fs1 en Fs2, de normaalkracht Fn en de zwaartekracht op het been Fz. Beide spankrachten zijn spierkrachten die elk een gevolg zijn van contractie van spierweefsel tussen het bekken (en lage wervelkolom) en het aangrijpingspunt van de betreffende krachtvector in de figuur. De normaalkracht is de reactiekracht in het heupgewricht. De lengtes a en b zijn afstanden van het aangrijpingspunt A van de normaalkracht tot de werklijnen van spankracht Fs2 en de zwaartekracht.
a. Afgaand op wat de figuur laat zien is te concluderen dat de pijllengtes niet op schaal getekend zijn. Leg dit uit.


Op de bovenkant van de knieschijf werken ook krachten van spieren die met hun andere kant gehecht zijn aan het bovenbeen (en niet aan het bekken). Deze krachten maken daarom geen deel uit van de grootte en de richting van de spankracht Fs1 waarmee in deze opgave gerekend wordt.
Spankracht Fs1 is 150 newton (de kracht van alleen de musculus rectus femoris). De zwaartekracht op het hele been is 120 N. De lengtes a en b zijn respectievelijk 5,0 cm en 45 cm. Hoek α in de figuur rechts is 60°.
b. Bereken de spankracht Fs2.
c. Bereken de grootte van de normaalkracht Fn in het heupgewricht.
d. Welke richting heeft de normaalkracht? (Bereken hoek β.)
• Liftcabine - (dynamica)
Een liftcabine beweegt eenparig versneld. Boven in de cabine hangt een katrol waarover een soepel koord ligt. Het koord is verbonden met twee blokken A en B. Zie de figuur. De massa van het wiel en het koord zijn te verwaarlozen en het wiel kan wrijvingsloos draaien. Blok B is in rust ten opzichte van de vloer van de cabine.
Het hangend blok A heeft een massa van 2,5 kg. Blok B steunt op de vloer en heeft een massa van 5,0 kg. De scherpe hoek β die het koord bij blok B maakt met de verticale richting is 35°.
De versnelling van het geheel (lift en inhoud) bedraagt 1,2 m/s2 en is omlaag gericht.

a. Leg uit of de lift mogelijk omhoog of omlaag beweegt.
b. Bereken de grootte van de kracht die de vloer uitoefent op blok B.
c. Welke richting heeft deze kracht? (Bereken de hoek (δ) tussen de richting van de kracht en de vloer.)
• Luchtballon / Parachutist - (numerieke natuurkunde, dynamica)
 Een verzwaard, met lucht gevuld ballonnetje (totale massa 25 gram) wordt op een hoogte van 20 meter zonder beginsnelheid losgelaten. Aanvankelijk ondervindt de ballon alleen zwaartekracht en een omhoog werkende drijfkracht van 0,1 N. Het gezamenlijk effect van beide krachten is dat de ballon omlaag gaat bewegen. Als gevolg van deze beweging oefent de lucht nu ook een opwaarts gerichte weerstandskracht uit. De weerstandskracht, die de resultante is van een drukweerstandskracht en een wrijvingskracht, is bij benadering recht evenredig met het kwadraat van de snelheid:
Een verzwaard, met lucht gevuld ballonnetje (totale massa 25 gram) wordt op een hoogte van 20 meter zonder beginsnelheid losgelaten. Aanvankelijk ondervindt de ballon alleen zwaartekracht en een omhoog werkende drijfkracht van 0,1 N. Het gezamenlijk effect van beide krachten is dat de ballon omlaag gaat bewegen. Als gevolg van deze beweging oefent de lucht nu ook een opwaarts gerichte weerstandskracht uit. De weerstandskracht, die de resultante is van een drukweerstandskracht en een wrijvingskracht, is bij benadering recht evenredig met het kwadraat van de snelheid:
Fw = c · v2 met c = 0,0080 kg/m.
Door toename van de snelheid van de ballon neemt de weerstandskracht toe. De resulterende kracht op de ballon neemt hierdoor af. Wanneer de resultante van de drie krachten tot een verwaarloosbare grootte is gereduceerd, is de snelheid van de ballon (vrijwel) constant.
a. Schrijf een rekenmodel dat elke 0,050 seconde de versnelling, de snelheid, de hoogte en het tijdstip voor de beweging van de ballon berekent.
b. Pas het model aan om een werkend programma op je rekenmachine te krijgen.
c. Op welke hoogte wordt de daalsnelheid van de ballon constant? Beschouw daartoe de snelheid constant zodra zij 1,00 % of minder van de (asymptotische) eindsnelheid afwijkt.
De 'vrije val' van een parachutist
 (in natuurkundig opzicht is dit géén vrije val)
(in natuurkundig opzicht is dit géén vrije val)
Op een hoogte van 3000 meter 'springt' een parachutist (80 kg) zonder beginsnelheid uit een helikopter en maakt een val met gespreide armen en benen. Neem voor de drijfkracht 1,1 N en voor de evenredigheidsconstante c 0,25 kg/m.
d. Tot welke constante waarde zal de valsnelheid toenemen?
Op 800 m hoogte wordt de parachute geopend. Hierdoor neemt de snelheid van de parachutist plotseling sterk af. De hoge vertraging neemt vervolgens eerst snel en geleidelijk af, daarna nadert de daling van de parachutist opnieuw een eenparig verloop. De richting van de beweging blijft verticaal, ook bij de landing. In de laatste fase van de daling heeft de parachutist een constante daalsnelheid van 6,0 m/s.
e. Welke waarde heeft de evenredigheidsconstante c tijdens de daling met geopende parachute?
 • Motorrijder - (dynamica)
• Motorrijder - (dynamica)
Een motorrijder neemt met constante baansnelheid een cirkelvormige bocht in de rijweg. De cirkel heeft een straal van 140 m. Om de bocht zonder vallen en opstaan te nemen houdt de berijder zijn voertuig in een scheve stand van 20° ten opzichte van verticaal.
Hoe groot is de snelheid van de motorfiets?
• Noodlanding - (arbeid, energie)
Een sportvliegtuigje (1200 kg) heeft op 400 meter hoogte een snelheid van 33 m/s als de propeller stilvalt door een motorstoring. Gebruikmakend van de vleugelkleppen heeft de piloot invloed op de draagkracht op de vleugels en de luchtweerstand. Via een vrijwel rechtlijnige glijvlucht (hellingshoek 10°) weet hij het toestel veilig aan de grond te zetten met een aanvliegsnelheid van 25 m/s ofwel 90 km/h.
Bereken de gemiddelde wrijvingskracht die het vliegtuig in de glijvlucht ondervindt.

• Sprint - (kinematica)
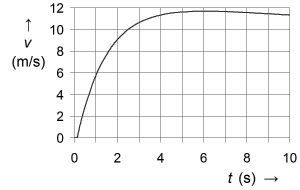 Een topatleet trekt een 100-meter-sprint over een recht baanvak. Na het startschot komt de hardloper pas in beweging nadat een reactietijd van 0,13 seconde is verstreken. Het diagram toont een aanvankelijk sterke toename van de snelheid en een aanhoudend afnemende versnelling. De grootste snelheid wordt op het tijdstip 6,05 s bereikt (11,68 m/s). In de laatste seconden van de rit verraadt een lichte daling van de snelheid een ingezette afname van het anaëroob vermogen van de atleet. Tenslotte passeert de renner de 100-meter-finishlijn met een snelheid van 11,34 m/s. Men klokt een tijd van 9,94 s.
Een topatleet trekt een 100-meter-sprint over een recht baanvak. Na het startschot komt de hardloper pas in beweging nadat een reactietijd van 0,13 seconde is verstreken. Het diagram toont een aanvankelijk sterke toename van de snelheid en een aanhoudend afnemende versnelling. De grootste snelheid wordt op het tijdstip 6,05 s bereikt (11,68 m/s). In de laatste seconden van de rit verraadt een lichte daling van de snelheid een ingezette afname van het anaëroob vermogen van de atleet. Tenslotte passeert de renner de 100-meter-finishlijn met een snelheid van 11,34 m/s. Men klokt een tijd van 9,94 s.
a. Hoe groot is de versnelling bij aanvang van de beweging?
b. Bepaal de verplaatsing van de atleet in de eerste seconde na het startsignaal.
c. Bepaal op welke afstand voor de eindstreep de sprinter zijn maximale snelheid heeft.
d. Met welke gemiddelde snelheid rent de hardloper de 100 meter?
• Verkeerslichtenregeling - (digitale signaalverwerking, logische schakelingen)
 Bij een nauwe brug zijn twee verkeerslichten opgesteld om het verkeer probleemloos langs de wegversmalling te leiden. In de animatie hiernaast is te zien hoe de verkeerslichteninstallatie reageert op verschillende verkeerssituaties.
Bij een nauwe brug zijn twee verkeerslichten opgesteld om het verkeer probleemloos langs de wegversmalling te leiden. In de animatie hiernaast is te zien hoe de verkeerslichteninstallatie reageert op verschillende verkeerssituaties.
De weg wordt niet druk bereden. Meestal is er geen verkeer; dan zijn beide verkeerslichten rood. Een naderend voertuig wordt opgemerkt door een sensor, of beter, door een elektrische schakeling die is uitgerust met enige sensoren in het wegdek (inductielussen). De sensorschakeling produceert een signaal waarna het automatische systeem vroeg of laat de aansturing van het overeenkomstige verkeerslicht activeert. Ongeacht de verkeerssituatie wordt een activeringspuls pas vrijgegeven als het andere verkeerslicht enige tijd rood is.
Het blokschema hieronder geeft globaal weer hoe verschillende onderdelen van de verkeerslichteninstallatie onderling communiceren.

De activeringspuls A1 start de cyclus rood-groen-geel-rood voor verkeerslicht 1. Signaalfunctie A1 heeft dan even de logische waarde 1, wat in het blokschema te herkennen is aan het blauw oplichten van de pijl bij uitgang A1. Het verdere verloop van de cyclus wordt gestuurd door een schakeling van logische verwerkers, waaronder een 4-bits-pulsenteller. Voor de eenvoud wordt hierna aangenomen dat de toestanden groen licht en geel licht even lang duren.
Enige terugkoppelingen ondersteunen het functioneren van de regeleenheid:
T1 is hoog zolang pulsenteller 1 telt;
G1 is hoog zolang verkeerslicht 1 groen heeft.
De signaalverwerking tijdens een verkeerslichtcyclus is in detail af te leiden uit het volgende schakelschema.

Schakelschema voor de verwerking van de cyclus rood-groen-geel-rood
Om in de stijl van het bekende systeembord te blijven zijn de meeste aansluitpunten via 'soepele snoertjes' met elkaar verbonden en is het verkeerslicht vervangen door een drietal leds (die hier zijn weergegeven met het symbool voor een signaallamp). Met de pulsgenerator ingesteld op 1 Hz komt een nabootsing van het verloop van de signaalverwerking redelijk overeen met het werkelijke verloop. Het signaal op ingang A1 kan met een drukschakelaar van het systeembord gesimuleerd worden.
| Waarheids- tabel XOF-poort |
||
| A | B | Y |
| 0 1 0 1 | 0 0 1 1 | 0 1 1 0 |
De functie van de XOF-poort kan met verschillende combinaties van de vertrouwde verwerkers EN, OF en NIET (invertor) worden nagebootst.
Vraag a.
Teken het schema van een logische schakeling die de XOF-waarheidstabel gehoorzaamt en waarin de verwerkers uitsluitend EN-, OF- of NIET-poorten zijn. Gebruik niet meer dan vijf verwerkers. Markeer de ingangen met A en B, de uitgang met Y.
Vraag b.
Er zijn meerdere ontwerpjes te bedenken die voldoen als antwoord op vraag a. Teken een schema van een tweede schakeling die de XOF-poort kan vervangen en maximaal vijf verwerkers bevat.
Met behulp van het schakelschema en de waarheidstabellen van alle erin voorkomende verwerkers kan een waarheidstabel voor een verkeerslichtcyclus worden opgesteld. In de tabel hieronder ontbreken nog de logische waarden van de uitgang van de XOF-poort en de uitgangen voor groen, geel en rood licht.
| Waarheidstabel voor de cyclus van een verkeerslicht | ||||||
| stap | pulsenteller | geheugencel | XOF | groen | geel | rood |
| 1 2 3 4 5 | 0000 0001 0010 0011 0100 | 0 → 1 1 1 1 1 → 0 | ... ... ... ... ... | ... ... ... ... ... | ... ... ... ... ... | ... ... ... ... ... |
Zodra de decimale waarde 4 in het display van de pulsenteller verschijnt volgt ogenblikkelijk een reset en wordt het tellen gestopt (zie het schakelschema). Stap 5 is dus van zeer korte duur (en een stap 6 wordt nooit bereikt). De stappen 2, 3 en 4 duren even lang. Het tijdsinterval wordt hier immers volledig bepaald door de ingestelde frequentie van de pulsgenerator.
De duur van stap 1 is in opeenvolgende cycli echter niet vanzelfsprekend even lang.
Vraag c.
Hoe lang kan stap 1 zoal duren? Geef een tijdsinterval van mogelijke waarden en verklaar de keuze van de kleinste en de grootste waarde van het interval. Gebruik als tijdseenheid de duur van stap 2 (één seconde).
Vraag d.
Maak de waarheidstabel voor de cyclus van een verkeerslicht compleet: neem de tabel over en vul op de open plaatsen de juiste logische waarde in (een 0 of een 1).
De praktische uitvoering van een ontwerp op papier verloopt soms minder gladjes dan verwacht. Door tijdsverschillen in signaalverwerking kan de schakeling bij de overgang van de gele naar de rode fase een zeer kort signaal voor groen licht afgeven. Hoewel de groene flits mogelijk voldoende weinig zichtbaar blijft, is de aansturende puls toch ongewenst omdat de terugkoppeling erdoor verstoord raakt. Het valse groen ontstaat als het systeem de EN-poort voor groen licht evalueert voordat de logische status van beide ingangen van de poort is bijgewerkt.
Vraag e.
Verklaar in detail het optreden van de korte puls voor vals groen licht. Ga daartoe eerst na hoe de logische waarden van de twee ingangen van de EN-poort voor groen licht achtereenvolgens veranderen als het verkeerslicht van de gele fase overgaat naar de rode.
Met een extra invertor in de schakeling is de kans op het optreden van een hoog signaal voor groen licht zo goed als nul zolang de binaire waarde van de pulsenteller niet 0001 is. Een aangepast schema staat hieronder.

Een aangepast ontwerp voor de cyclusverwerking
Vraag f.
Een hoog signaal G1 tijdens de overgang van de fase geel naar rood mag in de aangepaste schakeling zelfs volledig worden uitgesloten. Leg dit uit.
De twee sensorschakelingen leveren aan de regeleenheid een digitaal signaal af dat óf hoog óf laag is. Alle ingangssignalen kennen dus uitsluitend de logische waarden 0 en 1, en er is geen comparator nodig. De regeleenheid controleert voortdurend de logische status van de zes ingangen en laat op grond van de binnenkomende informatie en enige voorwaarden al dan niet een activeringssignaal uitgaan.
De regeleenheid hoeft niet te voorkomen dat een overbodige groene fase kan volgen als een automobilist een geel licht nadert en doorrijdt.
Aan de werking van de verkeerslichtenregeling als geheel zijn de volgende eisen gesteld:
- wanneer bij beide verkeerslichten groen licht gevraagd wordt krijgt verkeerslicht 1 bij voorrang groen (uitvoering van deze voorrangsregeling kan optreden kort nadat een voertuig een geel of juist rood geworden verkeerslicht heeft genaderd);
- de afwikkeling van een cyclus rood-groen-geel-rood loopt nooit gelijktijdig bij beide verkeerslichten;
- een verkeerslicht is rood zolang de afwikkeling van de cyclus rood-groen-geel-rood voor het verkeerslicht niet plaatsvindt.
In de volgende figuur zijn twee onderdelen van de regeleenheid getekend. De overige verwerkers ontbreken nog. Ook zijn nog niet alle verbindingen getekend.

Vraag g.
Neem de figuur over en teken daarin de ontbrekende verwerkers en de benodigde verbindingen om de regeleenheid in het automatische systeem goed te laten werken.
In de verkeerslichteninstallatie is voortdurend tenminste één van de twee pulsentellers inactief. Het systeem moet dus ook te bouwen zijn met maar één pulsenteller die voor beide verkeerslichten kan worden ingezet. In het schakelschema hieronder is een mogelijk ontwerp van zo'n systeem weergegeven. Een zestal verwerkers is niet benoemd en twee verbindingen ontbreken nog (zie de acht vraagtekens).

Vraag h.
Met welke verwerkers op de zes aangegeven plaatsen kan de schakeling goed werken en welke twee verbindingen zijn daartoe nodig?
Vraag i.
Hoewel de oude regeleenheid nog goed kan functioneren in combinatie met het één-pulsenteller-systeem, is toepassing van een in verschillende opzichten gunstiger ontwerp toch wenselijk. Welke veranderingen moeten daartoe worden doorgevoerd in het ontwerp van de oude regeleenheid?
• Warmtewisselaar - (warmte)
 In een bepaalde warmtewisselaar wordt de warmte volgens het tegenstroomprincipe overgedragen van een olie op water. Vereenvoudigd voorgesteld bestaat de warmtewisselaar uit twee concentrische buizen. 'n Opengewerkt gedeelte zie je hiernaast.
In een bepaalde warmtewisselaar wordt de warmte volgens het tegenstroomprincipe overgedragen van een olie op water. Vereenvoudigd voorgesteld bestaat de warmtewisselaar uit twee concentrische buizen. 'n Opengewerkt gedeelte zie je hiernaast.
De olie stroomt met een massadebiet van 20 kg/s door de binnenbuis en koelt daarbij af van 120 °C tot 50 °C. Het water stroomt in tegengestelde richting door de ruimte tussen de binnen- en de buitenbuis (12 kg/s). De temperatuur van het binnenkomende water is 10 °C. De soortelijke warmte van het water is 2,2 keer zo groot als die van de olie. Hoewel de warmtewisselaar aan de buitenkant geïsoleerd is gaat toch 4 % van de door de olie overgedragen warmte verloren aan de omgeving.
Bereken de temperatuur van het uitstromende water.
• Waterput - (kinematica, numerieke natuurkunde)
Om de diepte van het wateroppervlak onder de rand van een put te bepalen laat men een steen in de put vallen en meet men de tijd die verstrijkt tussen het loslaten van de steen en het horen van de plons. De gemeten tijdsduur bedraagt 3,0 seconde. Een herhaling van het experiment levert dezelfde meetwaarde op.
a. Hoe diep staat het waterniveau onder de rand als verondersteld wordt dat de geluidssnelheid oneindig groot is?
In werkelijkheid is de valtijd van de steen kleiner dan de gemeten 3,0 s. Een gedeelte van de waargenomen tijdsduur is immers nodig voor de verplaatsing van geluidsgolven van het wateroppervlak naar de bovenrand van de put.
b. Bereken opnieuw het verschil in hoogte tussen de rand en de waterspiegel, ditmaal rekening houdend met een reŽle geluidssnelheid van 340 m/s.
| Het verloop van een iteratie | |||
| rekenlus | hoogte (m) | stijgtijd geluid (s) | valtijd steen (s) |
| – 1 2 3 4 5 |
– 44,145 ... ... ... ... |
– 0,12984 ... ... ... |
3,0000 2,8702 ... ... ... |
c. Bereken de in vraag b gevonden hoogte (diepte) via een numerieke (iteratieve) rekenmethode. Verzamel de tussenwaarden in een tabel (zoals in het bijgaand exemplaar is aangegeven).
De iteratie kan ook stap voor stap gevolgd worden met een eenvoudig programma voor de rekenmachine. Hieronder volgt een voorbeeld voor een rekenmachine van Texas Instruments.
PROGRAM: WATERPUT
:3→C (de pijl verschijnt na een druk op de "STO>"- of store-toets)
:340→V
:9.81→G
:C→T
:Lbl 1 (Lbl vind je 'onder' de PRGM-toets)
:
:
:Disp H,T,"
:Pause
:Goto 1
:End
In de rekenlus tussen Lbl 1 (label 1) en Goto 1 zijn twee regels niet ingevuld.
Als het complete programma gestart wordt verschijnen de waarden voor de valhoogte en de valtijd van de eerste rekenlus in het display. Na een druk op de ENTER-toets volgen de waarden van de tweede lus eronder. Enzovoort.
Het programma slaat de laatst berekende waarden voor de hoogte en de valtijd op in de geheugens H en T (om ze vervolgens met Disp H,T te tonen). Het tijdsinterval waarin het geluid zich naar boven verplaatst wordt niet opgeslagen.
d. Vul het ontbrekende gedeelte van het programma op de twee lege regels aan.
• Weerstandsnetwerkje - (elektriciteit)
 De afbeelding hiernaast toont het schakelschema van een eenvoudig elektrisch netwerk. De schakeling wordt gevoed door twee (ideale) gelijkspanningsbronnen A en B. Verder zijn er nog drie weerstanden R1, R2 en R3 opgenomen en is de schakeling geaard in een punt bij de negatieve pool van spanningsbron A.
De afbeelding hiernaast toont het schakelschema van een eenvoudig elektrisch netwerk. De schakeling wordt gevoed door twee (ideale) gelijkspanningsbronnen A en B. Verder zijn er nog drie weerstanden R1, R2 en R3 opgenomen en is de schakeling geaard in een punt bij de negatieve pool van spanningsbron A.
Bewering:
in weerstand R3 loopt de elektrische stroom van vertakkingspunt P in de richting van knooppunt Q (en dus niet van Q naar P) omdat de verhouding UA/UB = 5/6 groter is dan de verhouding R1/R2 = 10/30 = 2/6.
a. De onderbouwing van de bewering hierboven is nogal zuinig en laat te wensen over. Maak in een sluitende redenering duidelijk waarom de potentiaal in knooppunt P groter is dan in punt Q.
Bekijk daartoe eerst de potentialen in P en Q bij twee extreme waarden voor weerstand R3 (R3 oneindig groot en R3 = 0 Ω) en trek hieruit vervolgens een conclusie over welke potentiaal de hoogste is bij de gegeven R3 = 15 Ω.
b. Bereken de stroomsterkte in de weerstand R3.
Hint: U1 + U3 = UA en U1 + U2 = UA + UB.
c. Hoe groot is de potentiaal in punt Q?
• Zonnepaneel - (elektromagnetische straling, warmte)
 In de ruimte buiten de aarde is een zonnepaneel loodrecht op de invallende zonnestraling geplaatst. De intensiteit van de instraling aan zonzijde bedraagt 1,4 kW/m2. Aangenomen moet worden dat invallende straling aan beide zijden van het paneel volledig wordt geabsorbeerd. Verwaarloos echter de intensiteit van achtergrondstraling en straling afkomstig van andere hemellichamen dan de zon.
In de ruimte buiten de aarde is een zonnepaneel loodrecht op de invallende zonnestraling geplaatst. De intensiteit van de instraling aan zonzijde bedraagt 1,4 kW/m2. Aangenomen moet worden dat invallende straling aan beide zijden van het paneel volledig wordt geabsorbeerd. Verwaarloos echter de intensiteit van achtergrondstraling en straling afkomstig van andere hemellichamen dan de zon.
Vooropgesteld dat het paneel een goede warmtegeleider is en overal (vrijwel) dezelfde temperatuur heeft, welke temperatuur zal zich dan instellen als er geen elektrische energie wordt afgenomen?
n41 Basisvaardigheden - n42 Beweging - n43 Krachten in evenwicht - n44 Kracht en beweging
n45 Arbeid en energie - n46 De gang van lichtstralen - n47 Het gebruik van lenzen - n48 Elektriciteit
n51 Signaalverwerking - n52 Kromlijnige bewegingen - n53 Trillingen - n54 Golven - n55 Numerieke natuurkunde - n56 Elektromagnetisme - n57 Inductie en wisselstromen - n61 Gassen en vloeistoffen
n62 Energie en warmte - n63 Atoomfysica - n64 Radioactiviteit - n65 Kernfysica
(n1,n2-indeling)
n111 Basisvaardigheden - n112 Beweging - n113 Kracht, moment - n114 Arbeid, energie
n115,n116 Licht, Oogwerking - n117 Elektrische stroom - n121 Trilling, golf - n122 Geluid
n123 Elektromagnetisch spectrum - n124 Signaalverwerking - n131 Radioactiviteit
n132 Gassen, vloeistoffen - n133 Energie en warmte - n211 Kracht en impuls
n212,n213 Kracht en beweging, Elektrisch veld - n214 Magnetische velden
n215,n216 Inductie, wisselstromen, Numerieke natuurkunde
n221,n222 Atoomfysica, Kernfysica
Hein ten Horn
![]() Top | Physics | Home
Top | Physics | Home