
Een met helium gevulde rubberballon die wordt losgelaten verdwijnt redelijk snel de lucht in. Maar hoe hoog kan hij komen? Dat hangt onder andere af van de eigenschappen van het rubber van de ballon.
Als je een ballon opblaast neemt het volume natuurlijk toe. Voor de druk geldt een wat ingewikkelder verhaal: het kost relatief veel moeite om een beginnetje te maken, maar als de ballon eenmaal een centimeter of tien diameter heeft gaat het daarna veel gemakkelijker. Je kunt die 'veerkarakteristiek', het verband tussen de diameter en de overdruk van een ballon, gemakkelijk meten. De huis-tuin-en-keukenopstelling waar ik het mee deed zie je in figuur 1.

De overdruk in een ballon wordt niet zo heel erg groot, minder dan 10 kPa (een meter waterkolom), vandaar ook dat je met een simpele U-buis de druk goed kunt meten. Het resultaat voor één bepaalde ballon staat in de figuur. Het hangt vast af van het soort ballon, deze meting geldt alleen voor deze specifieke ballon.
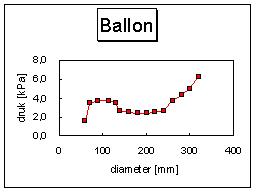
Uit de grafiek blijkt dat de ballon, redelijk opgeblazen tot een diameter van 20 cm, een overdruk heeft van 2.5 kPa (25 cm waterkolom). De absolute druk is dus vrijwel gelijk aan de luchtdruk buiten, 100 kPa. De ballon barstte bij een diameter van 33 cm en een overdruk van naar schatting 7 kPa.
Nu terug naar de oorspronkelijke vraag: hoe hoog komt de ballon? Als de ballon hoger komt neemt de luchtdruk af, en blaast de ballon zichzelf geleidelijk op. De absolute druk in de ballon wordt daarbij lager want volgens de gaswet is pV=constant (neem even aan dat de temperatuur geen invloed heeft en dat er geen gas weglekt) maar het drukverschil tussen 'binnen' en 'buiten' neemt toe. Bij de start is het volume van een ballon (20 cm) 42 cc. Als de ballon barst bij 33 cm is het volume ondertussen 190 cc. De absolute druk is dan dus 42/190 van wat het was, dus 23 kPa. Op dat moment is de verschildruk (zie grafiek) naar schatting 7 kPa, dus de buitendruk is 16 kPa.
Bij constante temperatuur (273 K) geldt voor de atmosfeer een drukafname met de hoogte (barometrische hoogteformule) volgens p = p0*exp(-0.12h) met h de hoogte in kilometers. Als je de druk 16 kPa daar invult kom je op 15 km.
Dat lijkt wel erg veel. Bovendien is bij die druk de opdrijvende kracht volgens de Wet van Archimedes ook te klein om de ballon naar boven te krijgen. Dat zou betekenen dat de ballon helemaal niet knapt, maar ergens halverwege op een evenwichtshoogte blijft hangen. Helemaal duidelijk is het niet. Karel Knip schreef er over op 28 april 2001 in de rubriek Alledaagse Wetenschap in de NRC (alleen toegankelijk voor abonnees).
Terug naar de homepage Orion
Terug naar Jurjen's homepage
Terug naar Physique Amusante