Ben's Hobbyhoekje -- Venn-diagrammen

Venn-diagrammen

In de wiskunde is een venndiagram een grafische voorstelling van de logische relaties tussen meerdere verzamelingen. Ze worden gebruikt in het onderwijs van elementaire verzamelingenleer en ter illustratie van eenvoudige relaties tussen verzamelingen in de kansrekening en de statistiek, de logica, de taalkunde en de informatica.

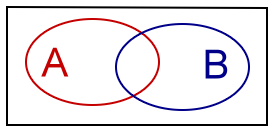In een Venn-diagram wordt een verzameling aangeduid met een gesloten kromme, meestal een cirkel of ellips. De elementen van die verzameling liggen binnen de kromme. Verzamelingen kunnen elkaar overlappen. Alles wat buiten de beschouwde verzamelingen valt, heet "universum". Dat wordt in het diagram aangeduid met een rechthoek. Het Universum wordt alleen in de figuur getoond als dat nodig is. Vaak wordt het weggelaten.

Als namen van de verzamelingen worden gewoonlijk (hoofd)letters gebruikt, die binnen de kromme worden geschreven. De naam van het universum wordt binnen of buiten de rechthoek geschreven, vlak naast een van de vier zijden.
Afzonderlijke elementen worden (als die binnen de figuur nodig zijn) aangeduid met een stip, al of niet met een naam erbij.
Een verzameling kan leeg zijn. Dat wordt genoteerd met het symbool Ø.

Venndiagrammen zijn genoemd naar de Engelse wiskundige en filosoof John Venn, die ze omstreeks 1880 bedacht. Charles Dodgson breidde het werk van Venn uit met het begrip universum.

Met verzamelingen kun je bewerkingen uitvoeren, naar analogie met de rekenkunde en de logica. Zie onderstaand overzicht. De "uitkomst" van de bewerkingen is grijs gekleurd in de Venn-diagrammen.

*Omschrijving, Notatie, Analogie*	*Venn-diagram*
Vereniging van `A` en `B`. Notatie: `A ∪ B` Analogieën: Optellen, Logisch `OR`
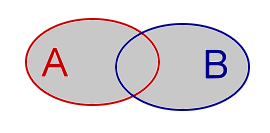Doorsnede van `A` en `B`. Notatie: `A ∩ B` Analogieën: Delen, Logisch `AND`
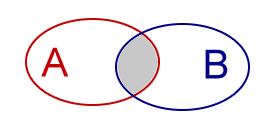Verschil van `A` en `B`. Notatie: `A \ B` Analogieën: Aftrekken
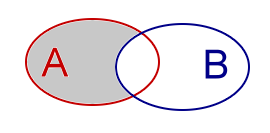Verzameling `A`. Notatie: `A` Analogieën: (geen)
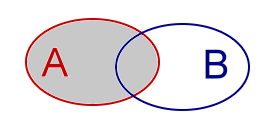Symmetrisch verschil van `A` en `B`. Notatie: `A Δ B` Analogieën: Logisch `XOR`
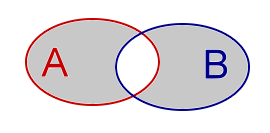Absoluut complement van `A` in `U`. Notatie: `U \ A` Analogieën: Aftrekken
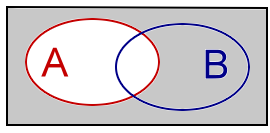`B` is deelverzameling van `A`. Notatie: `B ⊂ A` Analogieën: (geen)
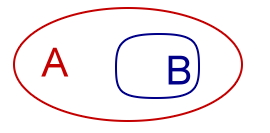Complement van `B` in `A`. Notatie: `A \ B` Analogieën: Aftrekken
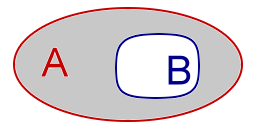`A` bevat deelverzameling `B` Notatie: `A ⊃ B` Analogieën: (geen)

Als B deelverzameling is van A, schrijf je: B ⊂ A. Als B géén deelverzameling is van A, schrijf je: B ⊄ A.

Als de verzameling A de verzameling B bevat, schrijf je: A ⊃ B. Als de verzameling A de verzameling B niet bevat, schrijf je: B ⊅ A.

Als element χ deel uit maakt van de verzameling A , schrijf je: χ ∈ A. Als element χ géén deel uit maakt van de verzameling A , schrijf je: χ ∉ A.

Opmerking:

Meer algemene informatie over verzamelingen vind je in het item Over verzamelingen. Informatie over toepassing van verzamelingen in JavaScript vind je in het item Over verzamelingen in JavaScript.