SummaryThe equation y=ax²+bx+c is a mathematical representation of all parabolas with the axis of symmetry parallel to the y-axis. To select a particular parabola from the set as a whole, the parameters a, b and c need to get the matching numerical values. So, if the program Parabola has to examine an individual case, it will ask the user to put in the three numbers. At first the quadratic equation ax²+bx+c=0 is evaluated. Using the values of a, b and c the program calculates the discriminant D and the real roots x1 and x2 (as far as they exist).
By request a diagram is shown. The following lines are displayed:
From now all calculator functions are available. Move the cursor along a line (left/right arrow), jump to another line (up/down arrow), scroll the diagram by moving the cursor position to the centre of the screen (ENTER) or put in an x-value and read off the new cursor coordinates at the bottom line. Perform calculations leading to for instance the coordinates of the parabola top or a point of intersection, or determine an area as done below (CALC, TABLE).
The coordinate axes Using D, x1, x2 Additional formulas Errors and peculiarities |
Program Listing[ Remarks ]PROGRAM:PARABOLA "Mem L3,L4,Y1-Y4,A-H,Y,Z" "ver200411" Normal:Float Full ClrHome Disp "** Parabola **","ax2+bx+c=0","parameters a,b,c" Disp "Output:","D, roots x1,x2","Draw graph of" Output(8,1,"(1:yes,0:no)") Input "y=ax2+bx+c ? ",G Lbl 1 ClrHome Disp "ax2+bx+c=0" Output(3,1,"(0:stop)") Input "a? ",Z If Z=0 Then ClrHome Stop End Z→A Input "b? ",B Input "c? ",C B^2–4AC→D .5/A→H Disp "D=" 10^int(log(max(10^-90,abs(D)))–7)→Z [ negation symbol (-) in "-90" ] [ subtraction symbol in "–7" ] Output(5,3,Zround(D/Z,0)) If D<0 Then Disp "Discriminant<0","No real roots" 1→E:1→F Else (-B–D^.5)H→E (-B+D^.5)H→F Disp "x1=","x2=" 10^int(log(max(10^-90,abs(E)))–6)→Z Output(6,4,Zround(E/Z,0)) 10^int(log(max(10^-90,abs(F)))–6)→Z Output(7,4,Zround(F/Z,0)) End Output(8,15,">>") Pause If G≠1 Goto 1 Sequential Func:RectGC CoordOn:GridOff AxesOn:LabelOff ExprOn:PlotsOff "AX3/3+BX2/2+CX"→Y4 FnOff GraphStyle(1,1) GraphStyle(2,1) GraphStyle(3,7) GraphStyle(4,1) "AX2+BX+C"→Y1 "2AX+B"→Y2 "C–(B2+1)/(4A)"→Y3 4→dim(L3) 4→dim(L4) min(0,-BH)→L3(1) max(0,-BH)→L3(2) 2abs(H)→Z If B=0 Then -Z→L3(1) Z→L3(2) End -.5DH→Y Y+3H→Z If D<0 2Y→Z Y–.5H→G min(min(0,G),min(Y,Z))→L3(3) max(max(0,G),max(Y,Z))→L3(4) L3(2)+L3(1)→L4(1) 1.5(L3(2)–L3(1))→L4(2) L3(4)+L3(3)→L4(3) 1.5(L3(4)–L3(3))→L4(4) L4/2→L4 L4(4)/L4(2)*94/62→Z If Z<1 L4(4)/Z→L4(4) If Z>1 L4(2)*Z→L4(2) If A>0 Then L4(3)+L4(4)→Z Else L4(3)–L4(4)→Z End (B^2–4A(C–Z))^.5/abs(A)→Z 2L4(2)/Z→Z 0→G If Z>5 Then 1→G 1.5L4(2)/Z→L4(2) End L4(1)–L4(2)→L3(1) L4(1)+L4(2)→L3(2) L4(3)–L4(4)→L3(3) L4(3)+L4(4)→L3(4) 10^int(log(max(10^-90,abs(L3)))–1)→L4 int(L3/L4)*L4→L3 L3(1)→Xmin L3(2)→Xmax L3(3)→Ymin L3(4)→Ymax max(10^-90,(Ymax–Ymin)/5)→Y 10^int(log(Y))→Z int(Y/Z)→Y If Y>5 5→Y If Y≠5 min(Y,2)→Y ZY→Xscl Xscl→Yscl ClrHome Disp "Lines to draw:","- y=ax2+bx+c","- dy/dx=2ax+b=y'" Disp "- directrix","- axes (y=0,x=0)","","info:" Output(8,1,"www.tenhorn.com") Output(7,15,">>") Pause ClrHome If G=1 Then Disp "(Axes differ)" Else Disp "(Axes equal)" End Disp "","Press TRACE,","left/right arrow","","(adjust WINDOW","or ZOOM)" Output(8,1,"") Stop
If you need help with programming your calculator, this exercise will put you on the way: Creating a Program for the TI-83 calculator |
Hein ten Horn
Top | Programs Texas Instruments | Home
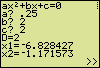
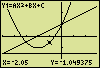



 At the graph screen you can retrieve these data to have a question answered. If you type for instance (E+F)/2 followed by ENTER, the parabola top is marked and the coordinates of the top are displayed at the bottom line.
At the graph screen you can retrieve these data to have a question answered. If you type for instance (E+F)/2 followed by ENTER, the parabola top is marked and the coordinates of the top are displayed at the bottom line.