Earth Centred Circular Motion of Artificial Satellites• What is the orbital radius of a GPS-satellite which makes one revolution within 11.967 h?
Find answers to questions like those above. Start up the program, select one of the following six orbital quantities and put in a value. From the given value your TI-calculator computes the remaining five quantities. An Illustrated ExampleTo take photographs of the earth's surface, a polar satellite has been put into orbit at an altitude of 800 km above the equatorial surface (thus having an orbital radius of
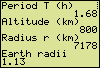
The next screen shows a period of 1.68 h, so one revolution lasts about 101 min. The orbital radius is displayed twice, once in km and once it is expressed as a number of earth radii. Likewise, the angular velocity is shown in the units rad/s and °/min. Special InputFeel free to put in an expression. For instance, if in an article on the International Space Station a period of 91.97 min is reported, the expression 91.97/60 is the most plausible input (in the unit hour). Similarly, convert an angular velocity of 0.00117 radian/second into °/min by multiplying it by the conversion factor 60*180/π. The factor is stored in memory X, so feed in either .00117*60*180/π or .00117X. Value of 'Big G'Nowadays Newton's gravitational constant G is a near four significant figures accurate quantity: (*) According to a new definition (International Astronomical Union, Prague, 24-08-2006) the Solar System consists of only eight planets, that is without Pluto. A planet is defined as a celestial body that (a) is in orbit around the Sun, (b) has sufficient mass for its self-gravity to overcome rigid body forces so that it assumes a hydrostatic equilibrium (nearly round) shape, and (c) has cleared the neighbourhood around its orbit. From now on Pluto is a member of a new class of objects called "dwarf planets". Influence of Sun and MoonGravitational forces in consequence of the presence of the sun and the moon are not taken into account. In lower orbits their influence is negligible. The resulting force of both sun and moon is maximal when the celestial bodies are in conjunction and at the same time their distances from earth are minimal. With an orbital radius less than 25 Mm the maximal resulting force will not exceed 1 % of the gravitational force of the earth (and will not exceed 5 % with radii less than 56 Mm). Fluctuations in the total force exerted on an orbiting artificial satellite remain below 1 % up to an orbital radius of 93 Mm (and below 5 % with a radius below 187 Mm). |
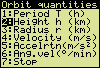
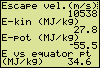
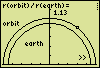
Program Listing[ Remarks ]PROGRAM:SATELLIT "Mem AEGHNRTVWXZ" "2000 ver2009" [ Memories, program version ] Normal:Float Full ClrHome Disp "** Satellite **","","Earth centred" Disp "circular motion","","","info:" Output(8,1,"www.tenhorn.com") Output(7,15,">>") Pause :ClrHome Disp "** Satellite **","","In the next" Disp "menu select a","known quantity." Disp "All others will","be calculated." Output(8,15,">>") 3.986004418*10^14→G [ *10^14 or E14 [ → : STO key ] 6378137→E 60*180/π→X Lbl 0 Pause :ClrHome Menu("Orbit quantities","Period T (h)",1,"Height h (km)",2,"Radius r (km)",3,"Velocity (m/s)",4,"Accelrtn (m/s2)",5,"Ang.vel(°/min)",6,"Stop",7) Lbl 7 ClrHome:Stop Lbl 1 Disp "Period" Input "T (hour)? ",T 3600T→T (G/4/π^2*T^2)^(1/3)→R Goto 8 Lbl 2 Disp "Altitude" Input "h (km)? ",H 1000H→H:H+E→R Goto 8 Lbl 3 Disp "Orbital radius" Input "r (km)? ",R 1000R→R Goto 8 Lbl 4 Disp "Orbital velocity" Input "v (m/s)? ",V max(abs(V),1)→V G/V^2→R Goto 8 Lbl 5 Disp "Centripetal","acceleration" Input "a (m/s2)? ",A max(abs(A),10^-15)→A (G/A)^.5→R Goto 8 Lbl 6 Disp "Angular velocity" Input "w (°/min)? ",W W/X→W (G/W^2)^(1/3)→R Lbl 8 If R<E Then ClrHome Disp "Your input","implies an orbit" Disp "below the equa-","torial surface." Disp "Intervention:","altitude = 0 km" Disp "Equat. radius:" Output(8,15,">>") Output(8,9,"km") Output(8,1,E/1000) Pause End max(R,E)→R (G/R^3)^.5→W:2π/W→T R–E→H:(G/R)^.5→V:G/R^2→A ClrHome Disp "Period T (h)" Disp round(T/3600,2) Disp "Altitude (km)" Disp round(H/1000,0) Disp "Radius r (km)" Disp round(R/1000,0) Disp "Earth radii" Output(8,1,round(R/E,2)) Pause :ClrHome Disp "Velocity v (m/s)" Disp round(V,0) Disp "Acceleratn(m/s2)" Disp round(A,3) Disp "Angular v(rad/s)" Disp round(W,6) Disp "Ang.vel. (°/min)" Output(8,12,round(WX,2)) Pause :ClrHome Disp "Escape vel.(m/s)" Disp round(2^.5*V,0) Disp "E-kin (MJ/kg)" Disp round(G/R/2/10^6,1) Disp "E-pot (MJ/kg)" Disp round(-G/R/10^6,1) Disp "E vs equator pt" Output(8,1,"(MJ/kg)") Output(8,12,round((-G/R/2–E^2*2.658747/10^9+G/E)/10^6,1)) Pause Sequential:Func RectGC:CoordOn GridOff:AxesOn LabelOff:ExprOff PlotsOff :FnOff 1.02→Z:-Z→Xmin Z→Xmax:.2→Xscl 0→Ymin:.2→Yscl 62Z/47→Ymax ClrDraw Circle(0,0,E/R) Circle(0,0,1) Circle(.6,.8,.024) Text(1,1,"r(orbit) / r(earth) = ") Text(7,52,round(R/E,2)) Text(18,1,"orbit") Text(max(38,24+iPart((1–E/R)*(53–24))),23,"earth") Text(52,77,">>") Goto 0
If you need help with programming your calculator, this exercise will put you on the way: Creating a Program for the TI-83 calculator |
Hein ten Horn
Top | Programs Texas Instruments | Home