Loop04

Een Loop-antenne

Hoofdstuk

4. Praktijktest en Conclusies

Praktijktest. Op 18 januari 2012 hoorde ik op 20 meter op mijn bazoka-dipool (gespannen op 8 - 12 - 8 meter +NAP) het station F4EQA met signaalsterkte S9. Op mijn loop (op 7 meter +NAP) was dit station te horen met S6, een geschat verschil van circa 3 S-punten (≈18 dB)? Bij het tunen bleek dat de SWR in de loopantenne beter was dan 1: 1,05. Hierdoor durfde ik met een gerust hart de maximaal 100 Watt uitgangsvermogen van de FT897 te gebruiken! Mijn eerste verbinding met deze loopantenne, waarbij ik nog wel vergat de loop op maximaal signaal uit te richten, kreeg ik als rapport S1!

Een latere vergelijking met mijn Perseus SDR, aangesloten op mijn actieve buitenantenne (type miniwipe pa0rtd, met een versterking van 0 dB), gaf bij ontvangst van een constante draaggolf maximaal 2 S-punten verschil (dus -12 dB) aan met de binnenshuis opgestelde loopantenne (volgens het schema van figuur 3).

Volgens de berekening van Koos, pa0kdf kun je uit de vermogensverhouding (tussen de verschillende antennes) een rendement schatten van de loopantenne, zodat:

“Uitgaande van de waarde van -12 dB, de vermogensverhouding 1/10^(12/10) of 0,063 bedraagt. Dat betekent 0,063e deel = 6,3% van het vermogen echt wordt uitgezonden. Immers van een normale dipool kunnen we aannemen dat het rendement er hoog is, dus bijna 100% wordt uitgezonden. Omdat de directivity van een loopantenne en van een dipool nauwelijks van elkaar verschillen kun je ze goed met elkaar vergelijken. Natuurlijk is die S-meter is niet zo nauwkeurig en moet je met die 12 dB de nodige slagen om de arm nemen.”

Uit het voorgaande trek ik de volgende conclusies:

Bij bij alle lengtes aan coaxkabel bij minimale C-waarde (dus op de hoogste frequenties) de reflectiedemping (Rd) het laagst was en dus de hoogste SWR gaf. Hoewel ..... -15 dB aan reflectiedemping geeft nog steeds maar een SWR van beter of gelijk aan 1 : 1,5!
De extra capaciteit van 158 pF, vooral aan de hoge zijde van het afstembereik, een beduidend hogere reflectiedemping veroorzaakte, maar bij nog grotere extra capaciteit weer lager werd.
Het tot een lus van twee windingen brengen van de langere coaxkabels veroorzaakte een kleine vermindering van het afstembereik maar wel een beduiden hogere reflectiedemping gaf. De LC verhouding speelt dus een grote rol.
Op de afgestemde frequentie de SWR laag genoeg blijft, meestal niet hoger is dan zo'n 1: 1,65 en zelfs op 20 meter 1: 1,2 (zie ook grafiek 1). Nog niet bekend is welk deel van het toegevoerde vermogen in de ringkern wordt opgesoupeerd.
Bij een lengte van 1,49 meter werd een Q gevonden welke in het midden van het afstembereik het hoogst was (1060). De Q varieerde in het afstembereik tussen 160 (40 meterband) en 355 (17 meterband). Ook werd de SWR en Q beïnvloed door de wijze van koppeling van het zendsignaal op de hele of halve winding (zie tabel 7)! Voor ontvangst maakte dat niet veel uit!

De lezer moet nu instaat zijn om met behulp van de tabellen 3, 4 en 6 de optimale lengte te bepalen voor zijn/haar gewenste afstembereik. Bij langere stukken coaxkabel is het, om de gehele lus hanteerbaar te houden, raadzaam om de kabel in een lus van minstens twee windingen brengen.
Natuurlijk wilde ik graag commentaar hebben op dit experiment. Nou, dat kreeg ik, o.a. van Koos, Pa0kdf. Zijn theoretische onderbouwing sprak mij wel aan en dat is de reden om ook zijn commentaar te vermelden. De vele grafieken van zijn Spice simulatie zouden dit verslag wel erg lang maken, vandaar dat ik volsta met de hoofdlijnen van zijn commentaar. Zijn originele documenten, met de resultaten in grafiekvorm, kunnen aan belangstellenden worden toegestuurd.

Eerste commentaar van Koos, pa0kdf, op dit experiment. Referte [2]. Koos stelt vast dat pa0mjk voor zijn berekeningen de volgende uitgangspunten gebruikt:

een vrij resonerende antennelus, waarbij het magnetische energie volledig in de antennelus wordt opgeslagen, en de elektrische energie in de afstemcondensator.
2. een aankoppeling via een zeer zwak gekoppelde lus.

De koppelfactor k wordt gedefinieerd als de verhouding van de gekoppelde magnetisch flux (door het koppellusje) tot de totale magnetische flux (van de antenneloop). De resonerende antennelus raakt op drie manieren zijn energie kwijt:

Door afstraling, bepaald door de stralingsweerstand R_rad.
Door verliezen in de lus: R_loss.
Door absorptie door de aankoppellus.

Die aankoppellus is verbonden met of de input impedantie van de Rx, of de output impedantie van de Tx. Kunnen we de input impedantie van de Rx wel redelijk goed benaderen met 50 ohm, bij de output impedantie van de Tx is dat niet het geval. Deze is onvoorspelbaar!

Input impedantie Tx aan de uitgang. In tegenstelling met wat we meestal denken, is de uitgangsimpedantie, zoals die bij het apparaat gespecificeerd wordt, niet de bronweerstand zoals we dat bij lineaire netwerken gewend zijn, maar een gespecificeerde afsluitimpedantie waarde, waarbij de Tx optimaal zijn vermogen kan afgeven, meestal met het hoogste rendement.
Echter, als je van buitenaf via de out-connector "naar binnen kijkt", dan zie je géén 50 ohm. Dat komt omdat je via het outputfilter naar een open collector kijkt van de eindtorren, en dat zijn feitelijk stroombronnen. De karakteristiek van een stroombron is dat bronimpedantie erg hoog is. De gespecificeerde uitgangsimpedantie heeft te maken met de optimale verhouding van spanning en stroom, waarbij de Tx zijn maximale vermogen kan leveren. Dit wordt weer bepaald door de hoogte van de voedingsspanning, de maximale stroom die de torren kunnen leveren, en de wikkelverhouding in de uitgangstransformator. Een zenderuitgang is dan ook geen lineair netwerk onderdeel.

Effect TX op belasting lusantenne. Door het gedrag van het uitgangsfilter, en de lengte van de tussenliggende coaxkabel, is de impedantie, die de koppellus belast, tamelijk onvoorspelbaar. Het is dus ook niet goed te voorspellen wat de invloed van koppellus is op de loopantenne. Als de impedantie zuiver reëel is, dan is er sprake van demping. Hoe groot die demping is, weten we niet. Is deze complex, dus capacitief of inductief, dan vindt er ook iets van verstemming van de loop plaats. Echter, gemiddeld genomen, varieert die impedantie, met een ruime speling, om de 50 ohm.
Bij gebrek aan betere informatie gaan we hierna ervan uit dat de belasting van de lusantenne door de Tx uitgang bepaald wordt door circa 50 ohm.

Eerste vervangingsschema loopantenne volgens figuur 4. Om bij een loopantenne een redelijk rendement te behalen weten we dat de verhouding tussen de opgeslagen energie in de antenne en de toegevoerde energie per periode, zijnde de Q-factor, zo hoog mogelijk moet zijn. Een kleine koppelfactor is dan al voldoende. Uit de trafotheorie weten we dat we een zwak gekoppelde spoelenset kunnen voorstellen door een serieschakeling van perfecte trafo (100% koppeling) met een niet-gekoppelde zelfinductie (zie figuur 5).

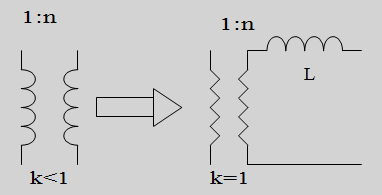
Figuur 5. Equivalentie van reële trafo naar perfecte trafo + seriezelfinductie.

In de schakeling van figuur 4 is dat ook letterlijk uitgevoerd. De trafo T1 kun je als die "perfecte" trafo beschouwen, met een wikkelverhouding van 4:2. Dat betekent dat je 50 ohm impedantie omlaag getransformeerd wordt naar: 50 * (2/4)^2 = 12.5 ohm! De coaxiaal uitgevoerde antennelus L vormt ook een trafo met een koppelfactor dicht bij 100%. Dat betekent dat je de secondaire van T1 net zo goed direct met de buitengeleider had kunnen verbinden. Sterker nog, dat was gunstiger geweest i.v.m. de ohmse verliezen in de relatief dunne binnengeleider. Het grote punt, waar het hier fout gaat, is dat de uitgang van T1 parallel staat over antenne L, i.p.v. in serie! Dus de lus wordt -parallel- belast met een impedantie van ruwweg 12,5 ohm. Dat is een hele zware belasting!

Het hele antennelus circuit, uitgaande van figuur 3, bestaat dan uit de serieschakeling van de zelfinducties van de antennelus L, spoel L2a, en capaciteit C1. Met daar al dan niet parallel L2b en C3. Aan deze seriekring zit dus de secondaire van T1 parallel aan L, en dus "getapt" op de totale resonantiekring.

Laten we even uitgaan van een omstrek van L van 1,5 m dat bij benadering een zelfinductie zal hebben van 1 µH. Met een zelfinductie waarde van L2a van 1,5 µH is de totale zelfinductie 2,5 µH. De parallelle impedantie van T1 wordt nu opgetransformeerd naar een impedantie welke parallel staat aan C1 van 12,5 * (2,5/1)^2 = 78 ohm.

Voor resonantie op 14 MHz moet C1 een waarde hebben van 52 pf. De √(L/C) verhouding wordt dan 220 ohm. Maar de parallelbelasting van de kring is al 78 ohm! Dus Q= 78/220= 0,35. Conclusie, zo kan dit circuit niet werken als bedoeld!

Metingen pa0kdf aan een coax-loop. Om te onderzoeken hoe dit circuit verder functioneert zijn eerst de eigenschappen de coaxiale antennelus L nagemeten. Aan een stuk ECOFLEX van 1,5 m lengte (vergelijkbare eigenschappen met RG8/RG213) werden m.b.v. de AIM4170 de volgende zelfinducties gemeten:

Door het diameterverschil heeft de binnengeleider een hogere zelfinductie dan de buitengeleider. Bij een 100% koppeling moet de zelfinductie nul zijn als de secondaire kant kortgesloten is. Dat is niet het geval, er blijft een ongekoppelde zelfinductie over. De koppelfactor halen we nu uit:

k_binnen-naar-buiten en k_buiten-naar-binnen moeten natuurlijk aan elkaar gelijk zijn, wat hier redelijk goed uitkomt.

Aangepast vervangingsschema. Dit betekent voor het vervangingsschema dat we de primaire zijde van L als transformator kunnen vervangen door een serie-zelfinductie van 0,33 µH, die dan in serie staat met de (typical) 12,5 ohm impedantie aan de uitgang van T1. We kunnen dan het eenvoudige vervangingsschema van figuur 4 verfijnen tot figuur 6:

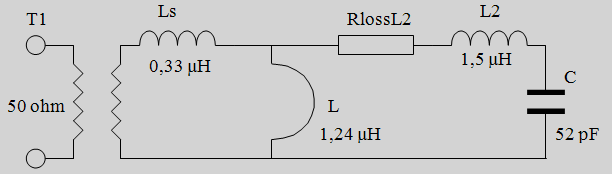
Figuur 6. Tweede versie vervangingsschema.

Hoe gaan nu daarin de stromen lopen? Daarvoor moeten we kijken naar de verschillende trillingsmodes, waarvan er al één is benoemd (I_k). De (hoofd-)stroom loopt rond door Llus, L2, R_lossL2 en C. Een andere trillingsmode is die, waarbij de stroomlus gevormd wordt door de secondaire van T1, inclusief Ls, RlossL2, L2, en C. Aangezien de reactantie van Llus circa 109 ohm bedraagt bij 14 MHz, veel hoger dan de tak door T1, is deze mode niet zo onwaarschijnlijk.