 |
Een Loop-antenne |
Hoofdstuk |
|
| 5. Simulaties en nawoord | |
|
Simulaties. Het in Spice ingevoerde schema voor een simulatie over frequentiebereik 10 - 18 MHz wordt getoond
in figuur 7. Uit de simulatie blijkt dat de stroom door de antenneloop en door Ls voor lage frequenties wel omhoog
gaat, maar dit is komt doordat de reactantie van Ls en Llus naar nul gaan. Er is daar geen sprake meer van een resonantie. De input
impedantie bij het resonantiepunt heeft een re le waarde van circa 3 ohm. | |
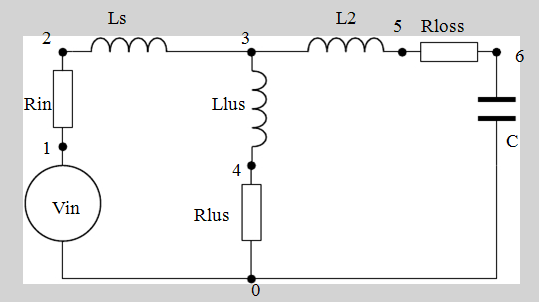 Figuur 7. Vervangingsschema in SPICE. | |
| Pa0wjg schrijft dat hij een goede aanpassing heeft bij resonantie. Dat betekent de re le waarde circa 12,5 ohm moet bedragen, uitgaande van de 2:1 transformatie in T1. De enige weerstand, waar ik bij deze simulatie die re le waarde van Zin kan be nvloeden, is de verliesweerstand van L2, cq. de Q-factor van L2. Ik had voor RlossL2 een waarde van 1 ohm aangenomen, overeenkomend met een Q-factor van L2 van 132. Dat was kennelijk te optimistisch. Gaan we spelen met de waarde van RlossL2, zo dat we voor de input impedantie van 12,5 ohm uitkomen, dan blijkt dat we voor RlossL2 7,8 ohm moeten invullen. De Q wordt dan 16,9. Dat lijkt laag, maar voor een luchtspoel niet onmogelijk. | |
|
Uitgestraald vermogen.
Uit de grafieken van de simulatie blijkt dat de stroom door de loopantenne niet piekt op de frequentie met de correcte aanpassing,
maar iets lager zit. De antenne loopstroom, bepalend voor de afstraling, bedraagt in de simulatie circa 12 mA bij een bronspanning van
1 Volt. Die bronspanning komt overeen met een klemspanning van 0,5 V aan de uitgang van T1, en dus weer met 1 V aan de ingang van T1,
met een ingangsimpedantie van 50 ohm.
Uitgaande van een zendvermogen van 100 Watt, betekent dat een spanning van 70,7 Volt over 50 ohm. Voor de stroom door de loop moeten we dus 12 mA vermenigvuldigen met 70,7, wat 849 mA oplevert. Het uitgestraalde vermogen kunnen we nu uitrekenen met de formule 1: | |
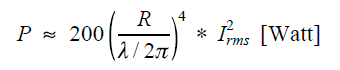 Formule 1. | |
| Daarin is R de straal van de loop. Die volgt uit de omtrek (1,5 m) en is dus 1,5/(2π)=0,2387 m. De golflengte λ bedraagt voor 14 MHz: 300/14 = 21.42 m. We kunnen dus invullen (formule 2): | |
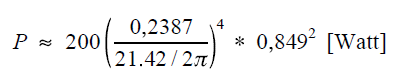 Formule 2. |
= 3,465 mWatt ! |
| Dat is 10*LOG(100/3,465E-3) = 44,6 dB beneden 100 Watt. | |
|
Pa0kdf concludeert: het zendvermogen wordt bijna helemaal opgestookt in L2. Deze 44,6 dB verschil lijkt erg veel, maar bij het test QSO met F4EQA
is het verschil 8 S-punten = 8*6=48 dB tussen het ene en het andere signaal. Er werd wel bij ontvangst een verschil van 18 dB aangegeven met de
dipool, maar of die dipool hangt precies in de verkeerde richting, of er is iets anders met je dipool aan de hand. Natuurlijk kan het zijn dat
deze simulaties een wat te pessimistisch beeld geven, en dat de inputgegevens niet helemaal correct zijn. Maar het geeft wel een aardig beeld
hoe de schakeling van figuur 2 en 3 functioneert. Ook de transformatie verhouding van T1 heeft grote invloed.
Hiermee is te begrijpen dat deze schakeling totaal anders in elkaar zit dan waar PA0MJK vanuit gaat.
Een tip is om de totale antenne eens door te zwiepen met een generator, of met de hand afgestemd, en daarbij een scoop met een oppiklus te gebruiken. Op deze wijze is het echte frequentiegedrag en de resonantiecurve te bepalen! | |
|
Aanvullende experimenten (Referte [4]: 2014_pa0kdf_Aanvulling 1.pdf).
In een viertal aanvullende experimenten is Rloss steeds aangepast om tot een goede SWR te komen. Dit betekent dat de waarde van R_loss
is gevarieerd opdat uit de simulatie de gewenste waarde van Rin komt. Deze komt dan overeen met de wikkelverhouding in T1, waarbij aan
de primaire zijde van T1 de impedantie 50 ohm wordt en dus de SWR 1:1,0 wordt.
Onderstaande tabel 8 vat de resultaten samen. Het blijkt dat de Q-factor van de loop weinig invloed heeft. Dat komt omdat de serie resonantie van L2, Rloss, en C de grote bepalende factor is. Impedantie verlaging komt dan ook de Q-factor van die seriekring ten goede, wat ook een positieve invloed heeft op de stroom door de antennelus. Merk wel op dat de stroom door de antennelus L steeds kleiner is dan die door L2. Dat betekent dat eigenlijk L2 als zendloop gebruikt moet worden i.p.v. L. | |
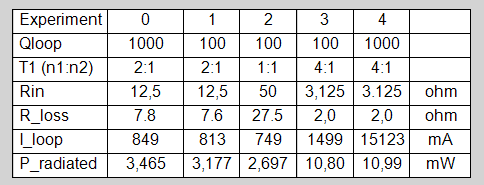 Tabel 8. Aanvullende experimenten van P_radiated versus Rin en Q. | |
| Vervolg aanvullende experimenten (Referte [5]: 2014_pa0kdf_Aanvulling 2.pdf). Bij deze experimenten is steeds de bronspanning aangepast voor een inputvermogen van 100 Watt, zodat op de plots de echte waarden van stroom en spanning zichtbaar zijn. De experimenten 5 t/m 8 van tabel 9 geven het resultaat van parallelvoeding met een hoge impedantie, waarbij de secondaire wikkeling van trafo T1 parallel is geschakeld is met de loop. | |
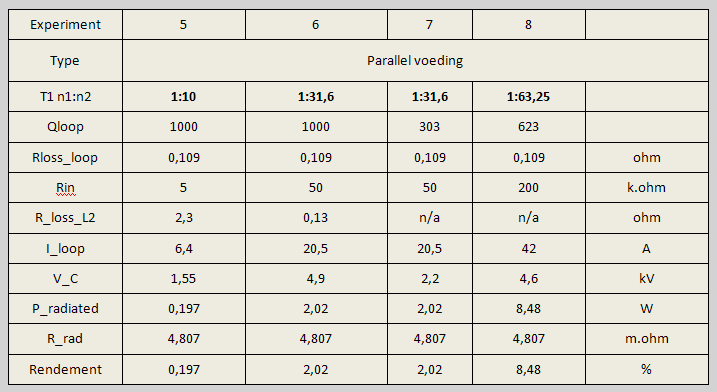 Tabel 9. Experimenten met parallel voeding met lage belasting van de loop L. | |
|
Een hogere impedantie van de parallelvoeding geeft wel een gunstiger resultaat, maar deze parallelle impedantie wordt al snel onpraktisch voor de realisering van T1. Met name de parasitaire wikkelcapaciteiten zullen boven een bepaalde trafoverhouding een grote rol gaan spelen. De experimenten 9 t/m 17 in tabel 10 geven het resultaten weer waarbij de secondaire wikkeling van trafo T1 in serie is geschakeld met de loop en met grotere loopafmetingen De serieschakeling van de secondaire van T1 met loop L functioneert ook. De functie van L2 is dan feitelijk niet aanwezig, maar draagt wel bij aan de verliezen. Bij een hogere omzetverhouding moet de verliesweerstand van L2 erg klein worden, c.q. de Q van L2 zeer hoog, dat dit niet meer realiseerbaar is. Zonder L2 kunnen we naar een lagere impedantie. Echter ook hier wordt de omzetverhouding onrealistisch hoog, waardoor de wikkelcapaciteiten het feestje gaan verpesten. Tenslotte het experiment (17) van een grotere loop met een omtrek van 5 meter, gelijk aan kwart golflengte van 20 meter. Dit is de maximale afmeting waarbij de loop in de praktijk nog net in afstemming gebracht kan worden. Zie dat dit de enige oplossing is met een redelijk goed rendement. Dat komt door de hoge stralingsweerstand, die stijgt met de vierde macht van de loopafmeting, hoewel de Q-factor hier vrij laag blijft! | |
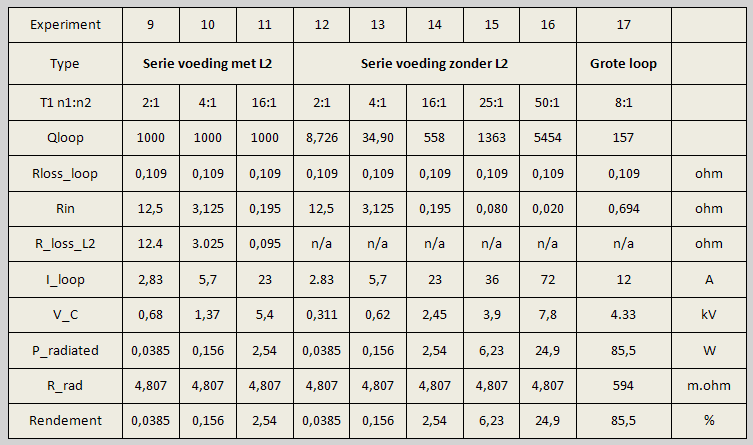 Tabel 10. In serie schakeling van de secundaire T1 met de Loop. | |
| Nawoord. Deze bijdrage is bedoeld om juist zonder al te veel theoretische kennis de zelfbouw met eenvoudige middelen te stimuleren. Het biedt daarmee een uitdaging aan andere lezers om hiermee verder te experimenteren. Wat verder het verschil in invloed is tussen een buiten antenne en een in huis opstelling laat zich ook nog raden! Het experiment en de geboden hulp gaf mij wel meer inzicht over het maken van een loopantenne en hoe je uit de tabellen de benodigde lengte kunt vaststellen voor het gewenste frequentiegebied. | |
|
Ook de valkuilen zijn mij nu duidelijk geworden: Houd wel, in verband met de stralingsveiligheid, bij het gebruik van een zendvermogen groter dan 20 Watt minimaal een afstand aan van minimaal 1 meter tot het vlak van de loop! Zelf ga ik weer aan de slag met een loop welke nu, ter vermindering van verliezen, NIET met pluggen wordt aangesloten en waarbij de inkoppeling in serie met de Loop staat. Mijn huidige loopantenne, met een doorsnede van circa 0,56 meter, is nu gebruiksgereed (zie foto 7). Ik wens nabouwers veel succes bij hun experimenten en hoop dat zij mij op de hoogte willen houden van hun ervaringen en (opbouwende) kritiek via:
pa0wjg @ veron.nl. | |
 Foto 7. Gebruiksgereed en maar wachten op DX! | |
Referte:
0-0-0 | |
|
| |
